Interquartile range in R

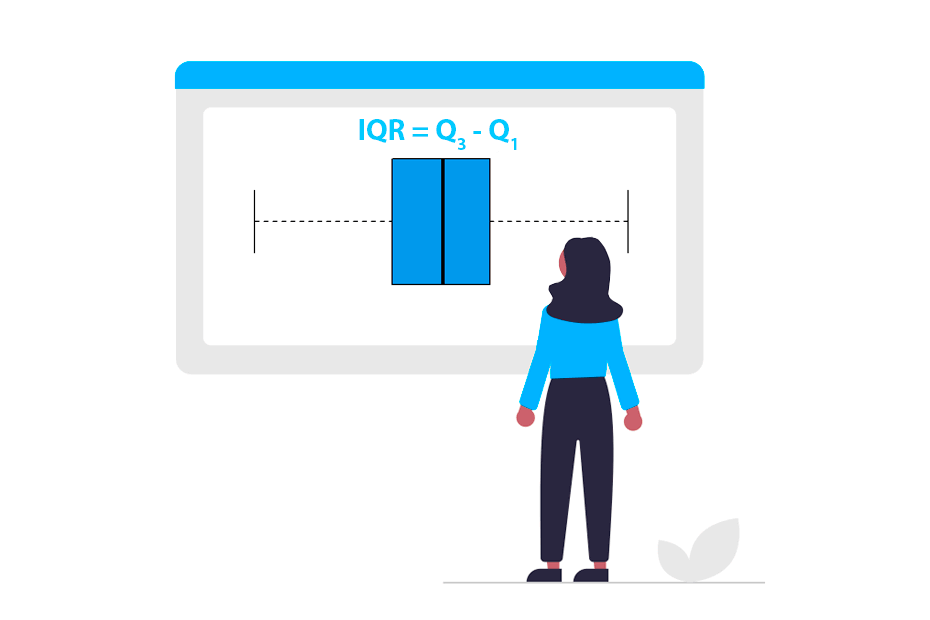
The interquartile range is a measure of statistical dispersion, specifically the difference between the third quartile (\(Q_3\)) and the first quartile (\(Q_1\)): \[IQR = Q_3 - Q_1\] This measured can be computed in R with the IQR function.

Syntax

The interquartile range can be computed in R with the IQR function, which has the following syntax:

IQR(x,             # Numeric vector
    na.rm = FALSE, # If TRUE, missing values are removed
    type = 7)      # Integer between 1 and 9 selecting a quantile algorithm

In the following section we are going to illustrate the usage of this function with some examples.

Examples

Interquartile range of a vector

Given a sample vector x you can input it to the IQR function to calculate its interquartile range:

# Sample data
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Interquartile range of 'x'
IQR(x)

16

The function return 16. Let’s compute it manually using the quantile function for a better understanding:

# Sample data
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Quartiles of 'x'
Q <- quantile(x)
Q

  0%  25%  50%  75% 100% 
 1.0  3.5 16.5 19.5 24.0 

The interquartile range is calculated as the third quartile (19.5) minus the first quartile (3.5), this is:

# Interquartile range of 'x'
Q[4] - Q[2]

# Equivalent to:
# quantile(x, probs = 0.75) - quantile(x, probs = 0.25)

75% 
 16 

Note that you can also specify other algorithm to compute quantiles making use of type, which takes an integer from 1 to 9 as input. The example below computes the interquartile range of x with the type 8 algorithm.

# Sample data
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Interquartile range of 'x' with Type 8 algorithm
IQR(x, type = 8)

17.33333

Interquartile range with missing values

If your data contains missing values you can set na.rm = TRUE in order to remove them from the computation.

# Sample data
x <- c(19, 21, NA, 1, 4, 2, NA, 24)

# Interquartile range of 'x' with missing values
IQR(x, na.rm = TRUE)

18

Interquartile range of the columns of a data frame

It is possible to calculate the interquartile range of the columns of a data frame using the apply function by columns as follows:

# Sample data
df <- data.frame(x = rnorm(10), y = rexp(10), z = runif(10))

# Interquartile range of the columns of a data frame
apply(df, 2, IQR)

        x         y         z 
2.6869600 0.6245126 0.3334760 

Semi interquartile range

The semi interquartile range (SIQR) is the interquartile range divided by two. This is:

\[SIQR = \frac{(Q_3 - Q_1)}{2}\]

See the example below for further clarification:

# Sample data
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Semi interquartile range of 'x'
SIQR <- IQR(x) / 2
SIQR

8