Coefficient of variation in R
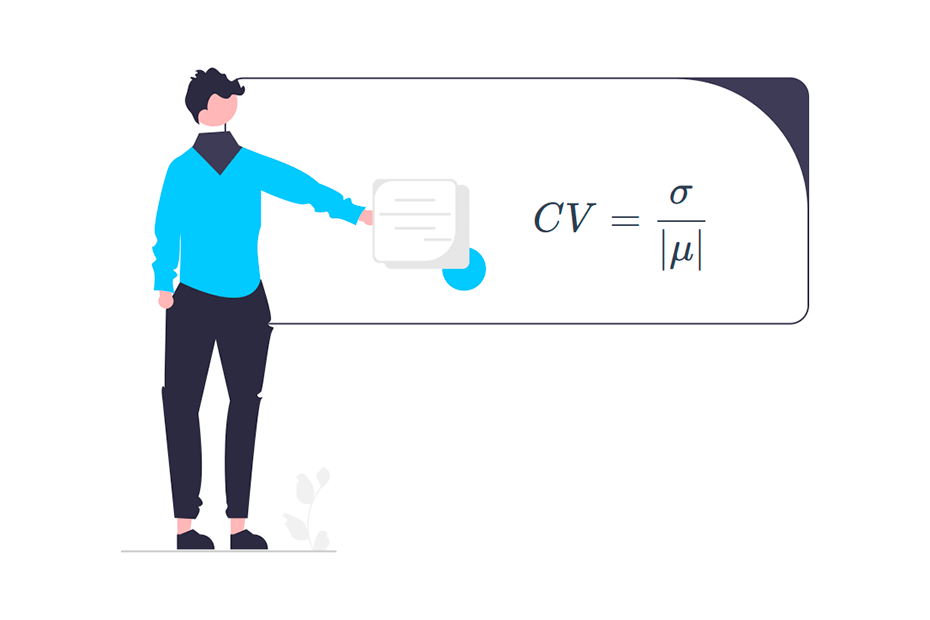
The coefficient of variation (CV) is a dispersion measure used to represent the relative variability of a dataset. It is calculated as the ratio of the standard deviation to the mean of a dataset, often expressed as a percentage.
This coefficient is an alternative to the standard deviation, as it allows to compare the variability among several datasets even if they have different scale or measurement units.
How to calculate the coefficient of variation?
The population coefficient of variation (CV) is the ratio between the standard deviation and the absolute mean:
\[CV = \frac{\sigma}{|\mu|}\]
The coefficient of variation is often expressed as a percentage, multiplying the ratio by 100:
\[CV = \frac{\sigma}{|\mu|} \cdot 100\]
For a sample, it is computed as the ratio between the sample standard deviation (\(S\)) and the sample mean (\(\bar{X}\)):
\[CV = \frac{S}{|\bar{X}|}\]
Notice that the mean must be different than 0.
In R, the coefficient of variation of a set of values can be computed calculating the ratio between the standard deviation with sd and the mean with mean.
# Sample data
x <- c(10, 30, 3, 44, 12, 15)
# Standard deviation and mean
sigma <- sd(x)
mu <- mean(x)
# Coefficient of variation
cv <- sigma / abs(mu)
cv0.797503If you want to calculate the coefficient of variation as percentage just multiply the previous result by 100:
# Sample data
x <- c(10, 30, 3, 44, 12, 15)
# Standard deviation and mean
sigma <- sd(x)
mu <- mean(x)
# Coefficient of variation in percentage
cv <- sigma / abs(mu) * 100
cv79.7503Function to compute the coefficient of variation
You can create your own function to calculate the coefficient of variation of a set of values.
The following block of code contains a function named cv that takes a vector as input and provides two additional arguments: percentage to calculate the coefficient as percentage when set to TRUE and na.rm to remove missing values if needed when set to TRUE.
# cv function
cv <- function(x, percentage = TRUE, na.rm = FALSE) {
cv <- sd(x, na.rm = na.rm)/abs(mean(x, na.rm = na.rm)) * ifelse(percentage, 100, 1)
return(cv)
}Making use of the previous function now you can compute the coefficient of variation in a single line:
# Sample data
x <- c(50, 48, 65, 13, 4, 19)
# Coefficient of variation
cv(x, percentage = TRUE)73.54353Recall to set percentage = FALSE if you don’t want to calculate the coefficient as percentage:
# Sample data
x <- c(50, 48, 65, 13, 4, 19)
# Coefficient of variation
cv(x, percentage = FALSE)0.7354353Comparing the coefficient of variation across groups
The principal use case of the coefficient of variation is to compare the dispersion between several datasets with different scale or measurement units. Consider the following data for two different groups:
| group1 | group2 |
|---|---|
| 19 | 160 |
| 30 | 290 |
| 12 | 280 |
| 56 | 330 |
As the scales between groups are different, calculating the standard deviation for each group will result in the second group having a higher standard deviation merely due to its scale. Therefore, comparing variability between groups won’t be possible.
# Sample data
df <- data.frame(group1 = c(19, 30, 12, 56),
group2 = c(160, 290, 280, 330))
# Standard deviation and mean by group
s <- rbind(apply(df, 2, sd), apply(df, 2, mean))
rownames(s) <- c("sd", "mean")
s group1 group2
sd 19.31105 73.25754
mean 29.25000 265.00000However, if you calculate the coefficient of variation for each group, the variability can be compared between groups, as this coefficient is relative.
# Sample data
df <- data.frame(group1 = c(19, 30, 12, 56), group2 = c(160, 290, 280, 330))
# Coefficient of variation for each column
# (using cv function defined in the previous section)
apply(df, 2, cv) group1 group2
66.02069 27.64435We can conclude that the first group has a higher variability (66.02%) than the second group (27.64%) despite the standard deviation of the second group was higher.