Test de Shapiro-Wilk en R
El contraste de Shapiro Wilk es un test utilizado para comprobar la normalidad de los datos, especialmente para conjuntos de datos pequeños, de 50 muestras o menos. En R, la función shapiro.test realiza este test para un vector numérico de valores.
Hipótesis
El contraste de hipótesis de Shapiro-Wilk comprueba la normalidad de los datos. La hipótesis nula (\(H_0\)) es que la distribución de la población es normal, mientras que la hipótesis alternativa es que la distribución de la población no es normal:
- \(H_0\): La distribución de la población es normal.
- \(H_1\): La distribución de la población NO es normal.
El test de Shapiro-Wilk se recomienda para conjuntos de datos pequeños, cuando el tamaño de la muestra es 50 o menos. Para conjuntos de datos más grandes se recomienda utilizar el test de Kolmogorov-Smirnov.
Comprobar normalidad e interpretación
Ejemplo con datos no normales
Considera un conjunto de datos de muestra con 30 valores extraídos de una distribución exponencial:
# Datos de muestra
set.seed(3)
x <- rexp(30)
# Histograma y densidad
hist(x, freq = FALSE, col = "white")
lines(density(x), lwd = 2, col = "red")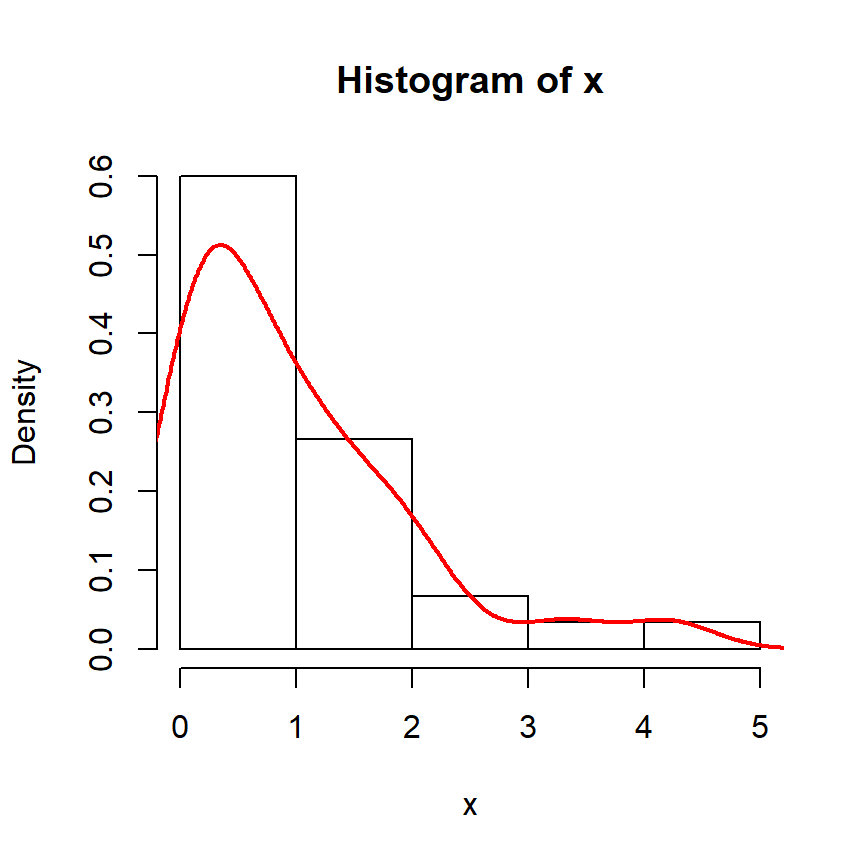
Si quieres comprobar si tus datos son normales, puedes introducirlos en la función shapiro.test, como se muestra a continuación.
# Datos de muestra
set.seed(3)
x <- rexp(30)
# Test de Shapiro-Wilk
shapiro.test(x) Shapiro-Wilk normality test
data: x
W = 0.83304, p-value = 0.0002792La función devolverá una lista formateada de clase "htest" con el nombre de tus datos, el valor del estadístico de Shapiro-Wilk (W) y el p-valor (p-value).
Para interpretar el resultado es necesario comparar el p-valor con un nivel de significación (\(\alpha\)), que es un umbral para determinar si una prueba es estadísticamente significativa o no. Los niveles de significación habituales son 0.1 (para un 90% de confianza), 0.05 (para un 95% de confianza), 0.01 (para un 99% de confianza).
Dado que el p-valor (0.000279) es inferior a los niveles de significación habituales (0.1, 0.05 y 0.01), tenemos pruebas significativas para rechazar la hipótesis nula de normalidad.
Si el p-valor es inferior a \(\alpha\) rechazamos \(H_0\) para el nivel de significación seleccionado.
Ejemplo con datos normales
Consideremos ahora unos datos de muestra extraídos de una distribución normal:
# Datos de muestra
set.seed(5)
x <- rnorm(50)
# Histograma y densidad
hist(x, freq = FALSE, col = "white")
lines(density(x), lwd = 2, col = "red")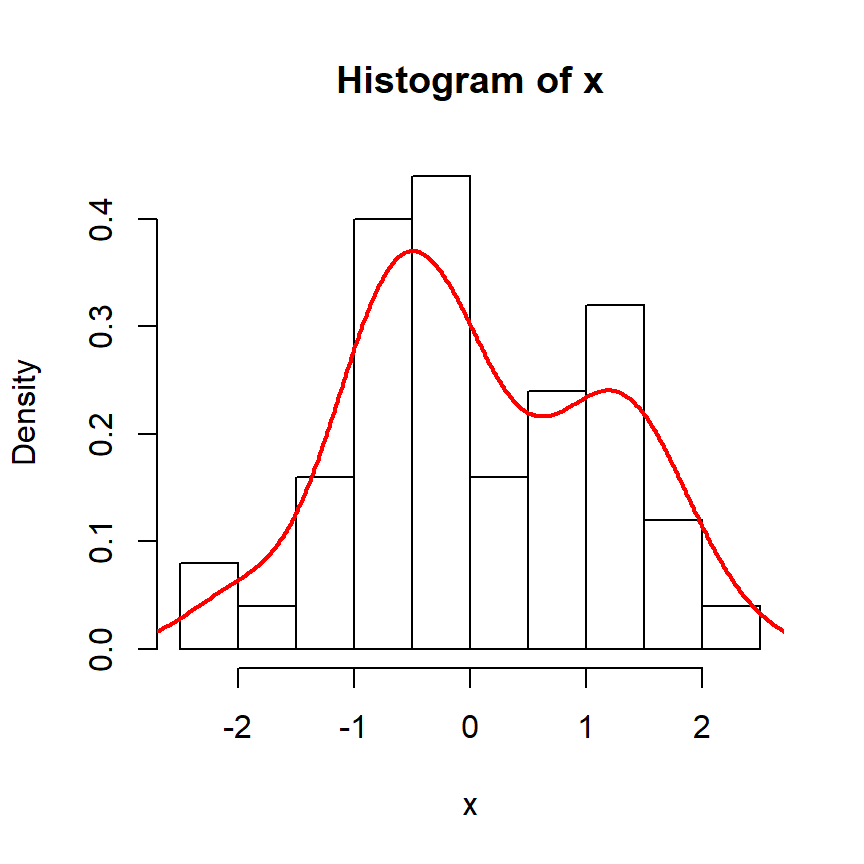
Si aplicas el contraste de Shapiro-Wilk a estos datos, obtendrás el siguiente resultado:
# Datos de muestra
set.seed(5)
x <- rnorm(30)
# Test de Shapiro-Wilk
shapiro.test(x) Shapiro-Wilk normality test
data: x
W = 0.95084, p-value = 0.178El p-valor es 0.178, superior a los niveles de significación habituales (0.1, 0.05 y 0.01), por lo que no tenemos pruebas suficientes para rechazar la hipótesis nula de normalidad.