Test de Lilliefors para la normalidad en R

La función lillie.test del paquete nortest se utiliza para realizar el test de Lilliefors, que es una versión modificada del contraste de normalidad de Kolmogorov-Smirnov.

Hipótesis

El contraste de Lilliefors es una variante de la prueba de Kolmogorov-Smirnov diseñada específicamente para comprobar la normalidad. Evalúa si los datos proceden de una distribución normal comparando la función de distribución empírica de los datos con la función de distribución acumulativa normal esperada.

La hipótesis nula de esta prueba es que la distribución de la población es normal, mientras que la hipótesis alternativa es que la distribución de la población no es normal:

• \(H_0\): la distribución de la población ES normal.
• \(H_1\): la distribución de la población NO ES normal.

Ejemplos e interpretación

Datos normales

Para este ejemplo, vamos a generar un conjunto de datos de muestra extraídos de una distribución normal. Los datos pueden examinarse visualmente mediante un histograma o un gráfico Q-Q para evaluar su normalidad:

# Datos de ejemplo
set.seed(17)
x <- rnorm(20)

# Dos columnas y una fila
par(mfrow = c(1, 2))

# Histograma y densidad
hist(x, freq = FALSE, col = "white")
lines(density(x), lwd = 2, col = "red")

# QQ-plot
qqnorm(x, pch = 16, col = 4)
qqline(x, col = "red", lwd = 2)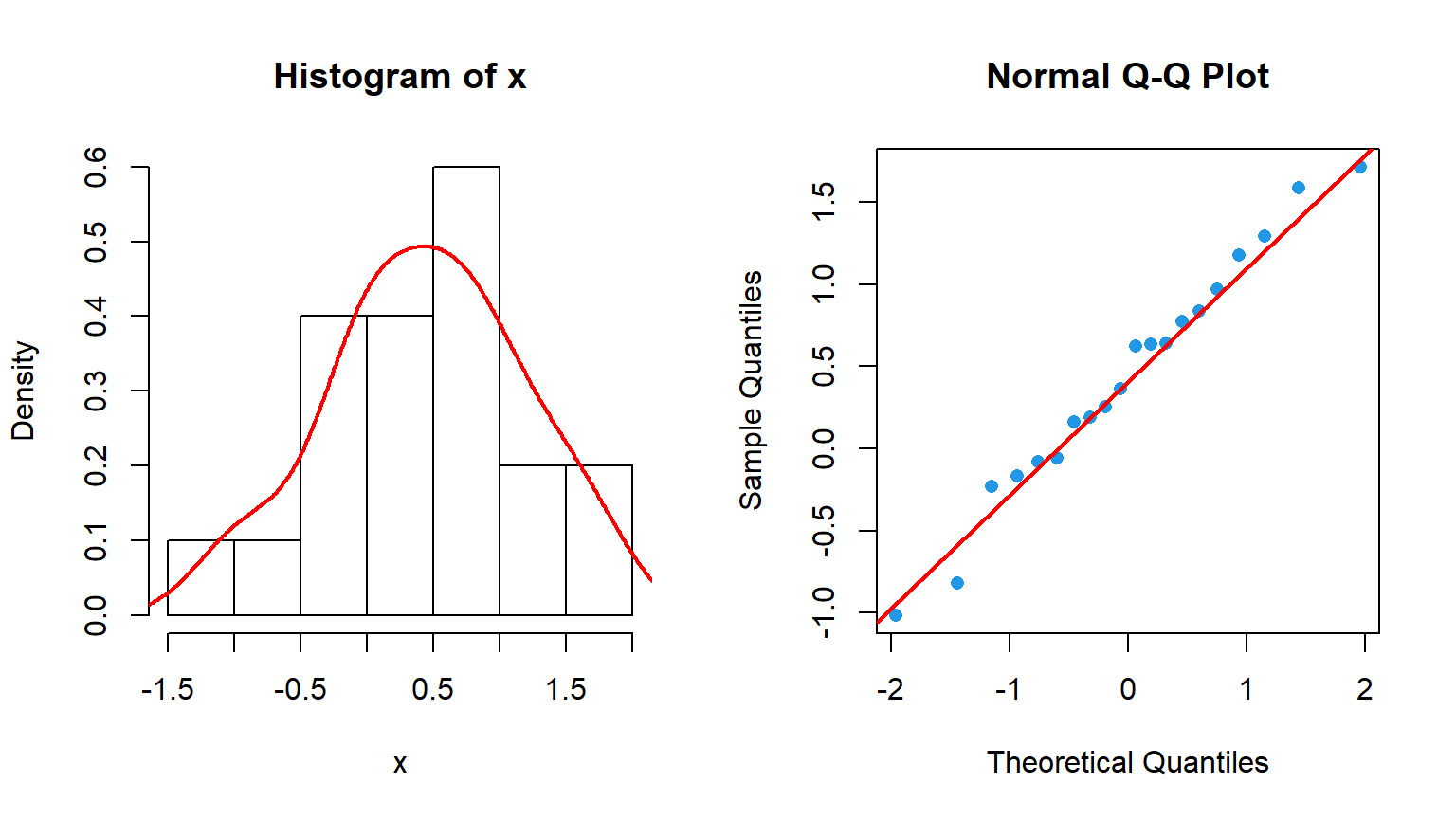

Ahora, se puede realizar el contraste de Lilliefors con la función lillie.test del paquete nortest para evaluar si la distribución poblacional de la variable x sigue una distribución normal:

# Datos de ejemplo
set.seed(17)
x <- rnorm(20)

# install.packages("nortest")
library(nortest)

# ¿Sigue 'x' una distribución normal?
lillie.test(x)

	Lilliefors (Kolmogorov-Smirnov) normality test

data:  x
D = 0.098636, p-value = 0.8775

El p-valor de 0.8775 sugiere que no hay pruebas estadísticas significativas para rechazar la hipótesis nula, lo que indica que la población probablemente se ajusta a una distribución normal.

Datos no normales

En este ejemplo vamos a utilizar datos extraídos de una distribución exponencial para comprobar cómo funciona la prueba:

# Datos de ejemplo
set.seed(17)
x <- rexp(20)

# Dos columnas y una fila
par(mfrow = c(1, 2))

# Histograma y densidad
hist(x, freq = FALSE, col = "white")
lines(density(x), lwd = 2, col = "red")

# QQ-plot
qqnorm(x, pch = 16, col = 4)
qqline(x, col = "red", lwd = 2)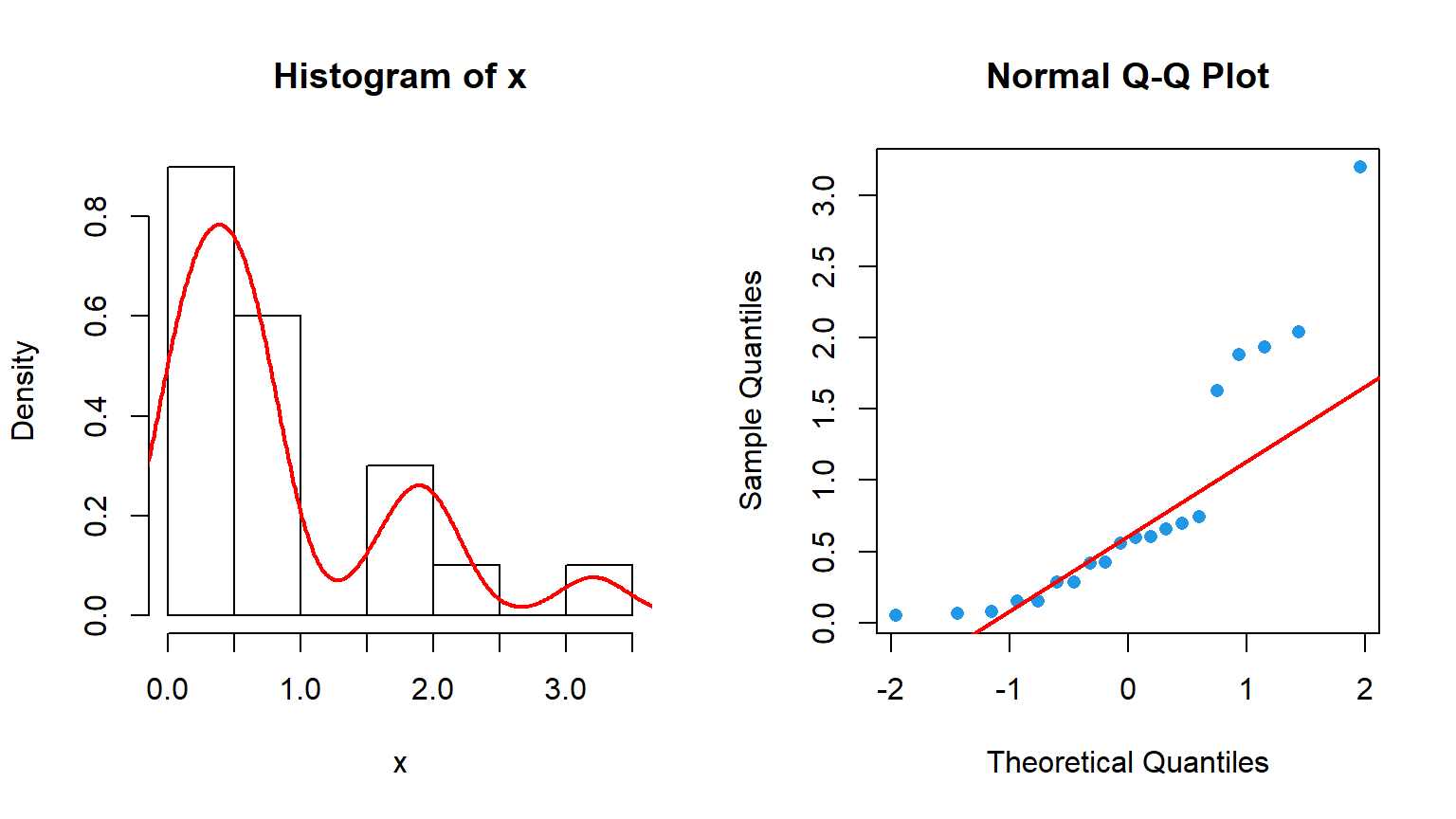

Con una inspección visual de los datos es posible ver que los datos podrían no seguir una distribución normal. Para comprobarlo puede realizarse el test de Lilliefors:

# Datos de ejemplo
set.seed(17)
x <- rexp(20)

# install.packages("nortest")
library(nortest)

# ¿Sigue 'x' una distribución normal?
lillie.test(x)

	Lilliefors (Kolmogorov-Smirnov) normality test

data:  x
D = 0.28833, p-value = 0.0001262

En este caso, el p-valor es inferior a los niveles de significación habituales (0.1, 0.05 y 0.01), por lo que hay pruebas sólidas en contra de la hipótesis nula de que los datos provienen de una distribución normal.