Distribución normal en R
La distribución normal o gaussiana es la distribución más conocida e importante en Estadística. En este tutorial aprenderás qué son y cómo utilizar las funciones dnorm, pnorm, qnorm y rnorm en R y las diferencias entre ellas. En consecuencia, aprenderás cómo crear y dibujar la distribución normal en R o RStudio, calcular las probabilidades bajo las curvas, los cuantiles, generación de números pseudoaleatorios normales e incluso cómo sombrear un área específica bajo una curva normal.
La distribución gaussiana
Entre las variables aleatorias continuas, la más importante es la distribución normal o gaussiana. Esta variable fue introducida por Carl Friedrich en el siglo XIX para estudiar las medidas de error.
Sea \(X \sim N(\mu, \sigma)\), es decir, una variable aleatoria con distribución normal de media \(\mu\) y desviación típica \(\sigma\):
- La función de densidad (o PDF, por sus siglas en inglés), también conocida como campana de Gauss, de \(x\) es \(f(x) = \frac{1}{\sqrt{2\pi \sigma^{2}}} e^{\frac{1}{2} (\frac{x - \mu}{\sigma})^2}\).
- La función de distribución acumulada (o CDF, por sus siglas en inglés) es \(F(x) = P(X \leq x)\).
- La función cuantil es \(Q(p) = F^{-1}(p)\).
- La esperanza y la varianza es \(E(X) = \mu\) y \(Var(X) = \sigma^2\), respectivamente.
En R existen las funciones dnorm, pnorm y qnorm, que permiten calcular la función de densidad, la de distribución y la cuantil normal para una serie de valores. Además, la función rnorm permite obtener observaciones aleatorias siguiendo una distribución normal. Las funciones relacionadas con la distribución normal se describen en la siguiente tabla:
| Función | Descripción |
|---|---|
| dnorm | Densidad normal (Función de densidad de probabilidad) |
| pnorm | Distribución normal (Función de distribución acumulada) |
| qnorm | Función cuantil de la distribución normal |
| rnorm | Generación de números pseudoaleatorios normales |
Por defecto, estas funciones consideran la distribución normal estándar, que tiene media 0 y desviación típica 1.
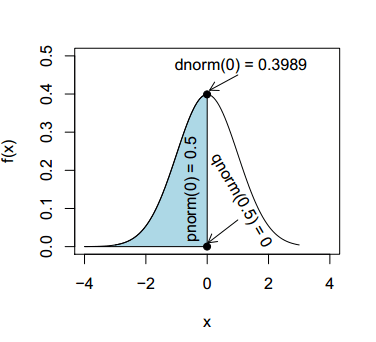
Aunque trataremos en detalle cada función en su correspondiente sección, en la siguiente ilustración puedes ver la relación entre las funciones dnorm, pnorm y qnorm:
La función dnorm
En R, puedes hacer uso de la función dnorm para calcular la función de densidad normal de parámetros \(\mu\) y \(\sigma\) para cualquier valor de \(x\).
dnorm(x, # Valores del eje X (rejilla)
mean = 0, # Número o vector representando la/s media/s
sd = 1, # Número o vector representando la/s desviación/es típica/s
log = FALSE) # Si TRUE, las probabilidades se devuelven como logaritmosConsidera, por ejemplo, que quieres crear la función de densidad de probabilidad normal para \(x \in (-4, 4)\), con media 1 y desviación típica de 3. Para calcularla, puedes escribir:
x <- -4:4
# x <- seq(-4, 4, length = 100) # Más observaciones
dnorm(x, mean = 1, sd = 3) 0.03315905 0.05467002 0.08065691 0.10648267 0.12579441
0.13298076 0.12579441 0.10648267 0.08065691También puedes especificar vectores en los argumentos mean y sd de la función. En el siguiente ejemplo, el valor de los elementos impares corresponde a \(\mu = 1, \sigma = 3\) y los pares a \(\mu = 2, \sigma = 4\).
dnorm(x, mean = c(1, 2), sd = c(3, 4))0.03315905 0.04566227 0.08065691 0.07528436 0.12579441
0.09666703 0.12579441 0.09666703 0.08065691Dibujar la distribución normal en R
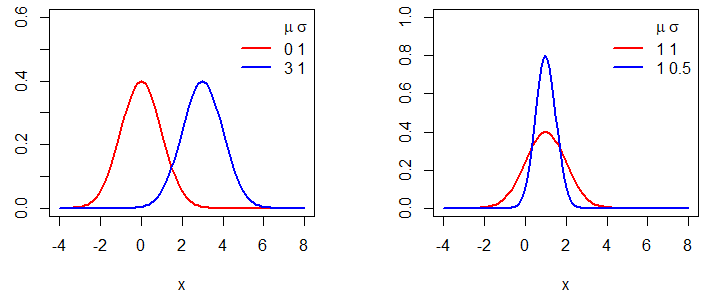
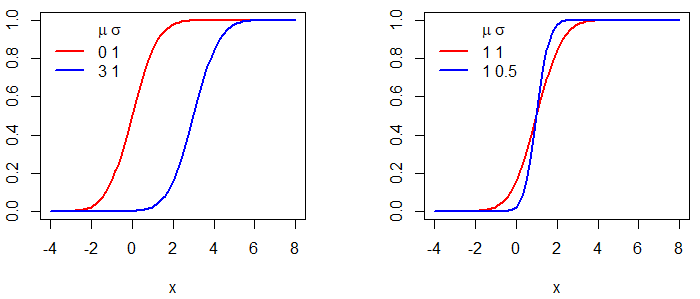
Crear un gráfico de distribución normal en R es fácil. Solo necesitas crear una rejilla (grid) para el eje X para el primer argumento de la función plot y pasar como entrada del segundo la función dnorm para la rejilla correspondiente. En el siguiente ejemplo mostramos cómo dibujar distribuciones normales para diferentes medias y varianzas.
par(mfrow = c(1, 2))
# Rejilla de valores para el eje X
x <- seq(-4, 8, 0.1)
#-----------------------------------------
# Misma desviación típica, distinta media
#-----------------------------------------
# Media 0, desviación típica 1
plot(x, dnorm(x, mean = 0, sd = 1), type = "l",
ylim = c(0, 0.6), ylab = "", lwd = 2, col = "red")
# Media 3, desviación típica 1
lines(x, dnorm(x, mean = 3, sd = 1), col = "blue", lty = 1, lwd = 2)
# Añadimos una leyenda
legend("topright", c(expression(paste(, mu, " ", sigma)), "0 1", "3 1"),
lty = c(0, 1, 1), col = c("blue", "red"), box.lty = 0, lwd = 2)
#-----------------------------------------
# Misma media, distinta desviación típica
#-----------------------------------------
# Media 1, desviación típica 1
plot(x, dnorm(x, mean = 1, sd = 1), type = "l",
ylim = c(0, 1), ylab = "", lwd = 2, col = "red")
# Media 1, desviación típica 0.5
lines(x, dnorm(x, mean = 1, sd = 0.5), col = "blue", lty = 1, lwd = 2)
# Añadimos una leyenda
legend("topright", c(expression(paste(, mu, " ", sigma)), "1 1", "1 0.5"),
lty = c(0, 1, 1), col = c("blue", "red"), box.lty = 0, lwd = 2)
par(mfrow = c(1, 1))La función pnorm
La función pnorm permite calcular la función de distribución acumulada (CDF, por sus siglas en inglés) de la distribución normal en R, que es la probabilidad de que la variable \(X\) tome valores menores o iguales que \(x\). La sintaxis de la función es la siguiente:
pnorm(q,
mean = 0,
sd = 1,
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) si FALSE
log.p = FALSE) # Si TRUE, las probabilidades vienen dadas como logaritmosComo ejemplo, teniendo en cuenta que la distribución normal es simétrica, la probabilidad de que la variable tome un valor inferior a la media es 0.5:
pnorm(0, mean = 0, sd = 1) # 0.5Ejemplo de la función pnorm
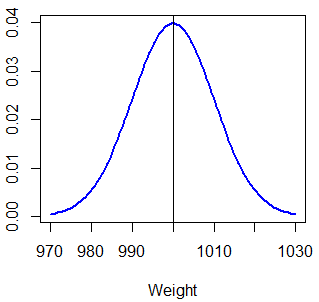
Ahora, supón que tienes una máquina que empaqueta arroz dentro de cajas. El proceso sigue una distribución normal y se sabe que la media del peso de cada caja es de 1000 gramos y la desviación típica es 10 gramos. Puedes dibujar la función de densidad normal en R escribiendo:
# Media y desviación típica
mu <- 1000
sigma <- 10
# Grid para una distribución normal no estándar
x <- seq(-3, 3, length = 100) * sigma + mu
# Función de densidad
f <- dnorm(x, mu, sigma)
plot(x, f, type = "l", lwd = 2, col = "blue", ylab = "", xlab = "Weight")
abline(v = mu) # Línea vertical en la mediaPrimero, si quieres calcular la probabilidad de que una caja pese menos de 1010 gramos (\(P(X < 1010) = P(X \leq 1010)\)), puedes escribir lo que sigue:
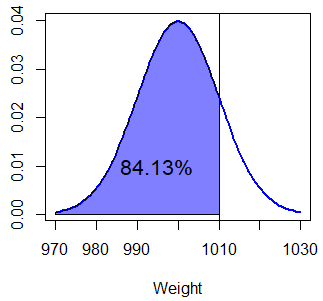
pnorm(1010, mu, sigma) # 0.8413447 o 84.13%
1 - pnorm(1010, mu, sigma, lower.tail = FALSE) # EquivalentePor lo que la probabilidad de que la caja pese menos de 1010 gramos es 0.8413 o 84.13%, que corresponde a el área de la siguiente ilustración:
lb <- min(x) # Límite inferior
ub <- 1010 # Límite superior
x2 <- seq(min(x), ub, length = 100) # Nueva rejilla
y <- dnorm(x2, mu, sigma) # Densidad
plot(x, f, type = "l", lwd = 2, col = "blue", ylab = "", xlab = "Peso")
abline(v = ub)
polygon(c(lb, x2, ub), c(0, y, 0), col = rgb(0, 0, 1, alpha = 0.5))
text(995, 0.01, "84.13%")Como sombrear el área debajo de la curva normal puede ser complicado y requiere varias líneas de código, hemos creado una función muy sencilla para lograrlo en una sola línea:
# mean: media de la variable normal
# sd: desviación típica de la variable normal
# lb: límite inferior del área
# ub: límite superior del área
# acolor: color del área
# ...: argumentos adicionales para ser pasados a la función lines
normal_area <- function(mean = 0, sd = 1, lb, ub, acolor = "lightgray", ...) {
x <- seq(mean - 3 * sd, mean + 3 * sd, length = 100)
if (missing(lb)) {
lb <- min(x)
}
if (missing(ub)) {
ub <- max(x)
}
x2 <- seq(lb, ub, length = 100)
plot(x, dnorm(x, mean, sd), type = "n", ylab = "")
y <- dnorm(x2, mean, sd)
polygon(c(lb, x2, ub), c(0, y, 0), col = acolor)
lines(x, dnorm(x, mean, sd), type = "l", ...)
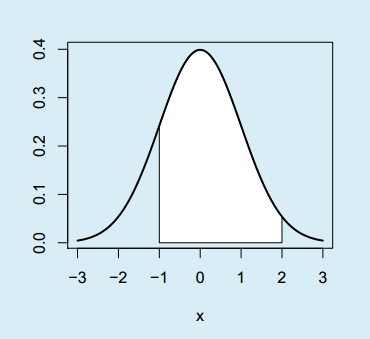
}Como ejemplo, si quieres sombrear el área entre -1 y 2 de una distribución normal estándar puedes escribir:
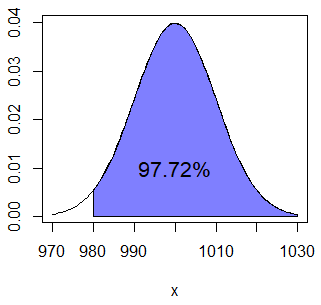
normal_area(mean = 0, sd = 1, lb = -1, ub = 2, lwd = 2, acolor = "white")Segundo, en caso de que quieras calcular la probabilidad de que una caja pese más de 980 gramos (\(P(X > 980) = P(X \geq 980)\)) puedes usar el argumento lower.tail.
pnorm(980, mu, sigma, lower.tail = FALSE) # 0.9772499 o 97.72%
1 - pnorm(980, mu, sigma) # Equivalente
pnorm(1020, mu, sigma) # Equivalente por simetríaLa probabilidad calculada corresponde al área:
normal_area(mean = mu, sd = sigma, lb = 980, acolor = rgb(0, 0, 1, alpha = 0.5))
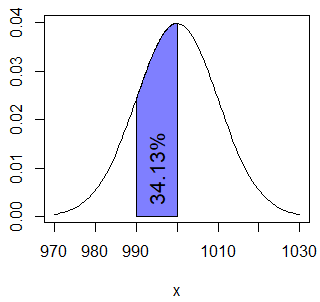
text(1000, 0.01, "97.72%")Por último, si quieres calcular la probabilidad de que una caja pese más de 990 gramos y menos de 1000 tienes que calcular \(P(X \leq 1000) - P(x \leq 990) = P(X < 1000) - P(x <990)\) y por tanto puedes ejecutar:
pnorm(1000, mu, sigma) - pnorm(990, mu, sigma) # 0.3413447 o 34.13%Puedes dibujar el área con el siguiente código:
normal_area(mean = mu, sd = sigma, lb = 990, ub = 1000,
acolor = rgb(0, 0, 1, alpha = 0.5))
text(995, 0.01, "34.13%", srt = 90)Para variables continuas, como \(P(X = x) = 0\), \(P(X \geq x) = P(X > x)\) y \(P(X \leq x) = P(X < x)\).
Graficar la función de distribución normal acumulada en R
Con la función pnorm también puedes dibujar la función de densidad acumulada de la distribución normal en R:
par(mfrow = c(1, 2))
# Rejilla de valores para el eje X
x <- seq(-4, 8, 0.1)
#-----------------------------------------
# Misma desviación típica, distinta media
#-----------------------------------------
# Media 0, desviación típica 1
plot(x, pnorm(x, mean = 0, sd = 1), type = "l",
ylim = c(0, 1), ylab = "", lwd = 2, col = "red")
# Media 3, desviación típica 1
lines(x, pnorm(x, mean = 3, sd = 1), col = "blue", lty = 1, lwd = 2)
# Leyenda
legend("topleft", c(expression(paste(, mu, " ", sigma)), "0 1", "3 1"),
lty = c(0, 1, 1), col = c("blue", "red"), box.lty = 0, lwd = 2)
#-----------------------------------------
# Misma media, distinta desviación típica
#-----------------------------------------
# Media 1, desviación típica 1
plot(x, pnorm(x, mean = 1, sd = 1), type = "l",
ylim = c(0, 1), ylab = "", lwd = 2, col = "red")
# Media 0, desviación típica 0.5
lines(x, pnorm(x, mean = 1, sd = 0.5), col = "blue", lty = 1, lwd = 2)
# Leyenda
legend("topleft", c(expression(paste(, mu, " ", sigma)), "1 1", "1 0.5"),
lty = c(0, 1, 1), col = c("blue", "red"), box.lty = 0, lwd = 2)
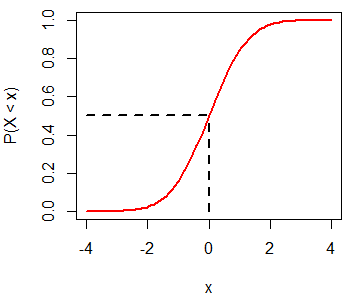
par(mfrow = c(1, 1))Recuerda que \(P(X < 0) = 0.5\) para una distribución normal estándar:
x <- seq(-4, 4, 0.1)
plot(x, pnorm(x, mean = 0, sd = 1), type = "l",
ylim = c(0, 1), ylab = "P(X < x)", lwd = 2, col = "red")
segments(0, 0, 0, 0.5, lwd = 2, lty = 2)
segments(-4, 0.5, 0, 0.5, lwd = 2, lty = 2)La función qnorm
La función qnorm permite encontrar el cuantil (percentil) \(Q\) para cualquier probabilidad \(p\).
En consecuencia, la función qnorm es la inversa de la función pnorm. La sintaxis de la función qnorm es como sigue:
qnorm(p, # Número o vector de probabilidades
mean = 0, # Número o vector representando la/s media/s
sd = 1, # Número o vector representando la/s desviación/es típica/s
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) si FALSE
log.p = FALSE) # Si TRUE, las probabilidades vienen dadas como logaritmosComo primer ejemplo, el cuantil para la probabilidad 0.5 (\(Q(0.5)\)) en una distribución simétrica es igual a la media:
qnorm(0.5, mean = 0, sd = 1) # 0Además, puedes obtener el cuantil para cualquier probabilidad dada. Nótese la relación entre las funciones pnorm y qnorm:
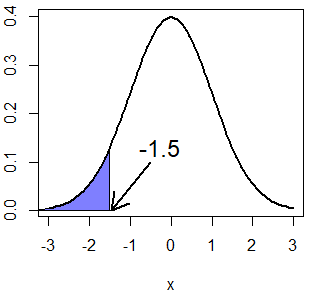
x <- pnorm(-1.5, mean = 0, sd = 1) # 0.0668072
qnorm(x, mean = 0, sd = 1) # -1.5
normal_area(mean = 0, sd = 1, ub = -1.5,
lwd = 2, acolor = rgb(0, 0, 1, alpha = 0.5))
arrows(-0.5, 0.1, -1.45, 0, lwd = 2, length = 0.2)
text(-0.25, 0.13, "-1.5", cex = 1.5)Si quieres calcular, por ejemplo, el cuantil \(Q(P(X > 1.5)) = Q(1 - P(X \leq 1.5)) = Q(0.067)\), puedes establecer el argumento lower.tail de la función como TRUE.
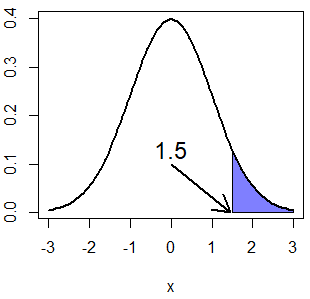
x <- pnorm(1.5, mean = 0, sd = 1, lower.tail = FALSE) # 0.0668072
qnorm(x, mean = 0, sd = 1, lower.tail = FALSE) # 1.5
# Equivalente a:
# x <- 1- pnorm(1.5, mean = 0, sd = 1)
# qnorm(1 - x, mean = 0, sd = 1)
normal_area(mean = 0, sd = 1, lb = 1.5, lwd = 2,
acolor = rgb(0, 0, 1, alpha = 0.5))
arrows(0, 0.1, 1.45, 0, lwd = 2, length = 0.2)
text(0, 0.13, "1.5", cex = 1.5)Dibujar la función cuantil normal
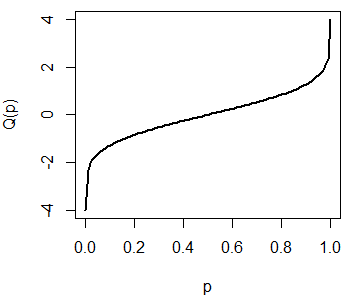
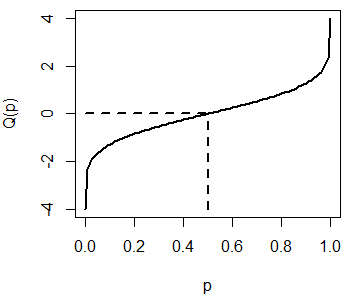
Puedes dibujar la función cuantil de una distribución normal estándar escribiendo lo siguiente:
plot(qnorm, pnorm(-4), pnorm(4), lwd = 2, xlab = "p", ylab = "Q(p)")
# Equivalente a:
# x <- seq(pnorm(-4), pnorm(4), length = 100)
# plot(x, qnorm(x, mean = 0, sd = 1), type = "l",
# lwd = 2, xlab = "p", ylab = "Q(p)")La gráfica anterior representa los posibles resultados de la función qnorm para la distribución normal estándar. Recuerda que \(Q(0.5) = 0\):
plot(qnorm, pnorm(-4), pnorm(4), lwd = 2,
xlab = "p", ylab = "Q(p)")
segments(0.5, -4, 0.5, 0, lty = 2, lwd = 2)
segments(0, 0, 0.5, 0, lty = 2, lwd = 2)La función rnorm
La función rnorm genera \(n\) observaciones de la distribución normal con media \(\mu\) y desviación típica \(\sigma\). La sintaxis de la función rnorm en R es la siguiente:
rnorm(n, # Número de observaciones a ser generadas
mean = 0, # Número o vector representando la/s media/s
sd = 1) # Número o vector representando la/s desviación/es típica/sPor lo tanto, puedes generar 10 observaciones de una distribución normal estándar en R con el siguiente código:
rnorm(10)0.3320065 -0.6454991 -0.3692699 -0.4160260 0.5756340
-0.8793241 -0.8095590 0.4926698 -0.8038873 -0.3446890Sin embargo, debe tenerse en cuenta que si no se especifica una semilla, la salida no será reproducible. Puedes utilizar la función set.seed para hacer que la salida sea reproducible:
# Semilla para reproducibilidad
set.seed(1)
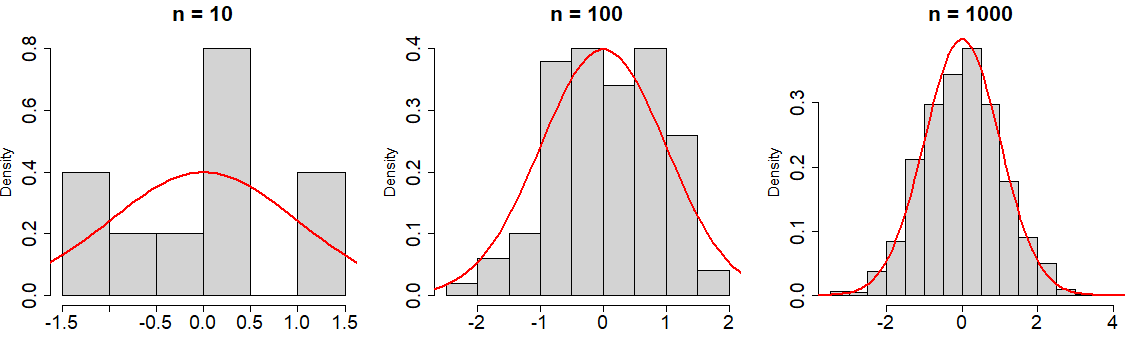
rnorm(1) # -0.6264538Además, en la siguiente gráfica puedes observar cómo al aumentar el número de observaciones, los histogramas de los datos se acercan a la función de densidad normal real:
# Dividimos la ventana gráfica en una fila y tres columnas
par(mfrow = c(1, 3))
x <- seq(-10, 10, length = 200)
# Semilla
set.seed(3)
# n = 10
hist(rnorm(10, mean = 0, sd = 1), main = "n = 10",
xlab = "", prob = TRUE)
lines(x, dnorm(x), col = "red", lwd = 2)
# n = 100
hist(rnorm(100, mean = 0, sd = 1), main = "n = 100",
xlab = "", prob = TRUE)
lines(x, dnorm(x), col = "red", lwd = 2)
# n = 1000
hist(rnorm(1000, mean = 0, sd = 1), main = "n = 1000",
xlab = "", prob = TRUE)
lines(x, dnorm(x), col = "red", lwd = 2)
# Volvemos a la ventana original
par(mfrow = c(1, 1))