Test de Kolmogorov-Smirnov en R con ks.test()

El contraste de Kolmogorov-Smirnov (KS) es una test genérico utilizado para comparar la distribución empírica de los datos con una distribución teórica o para comprobar si dos muestras siguen la misma distribución. R proporciona una función llamada ks.test para realizar esta prueba.

Sintaxis de ks.test

La sintaxis de la función ks.test es la siguiente:

ks.test(x, y, ...,
        alternative = c("two.sided", "less", "greater"),
        exact = NULL, simulate.p.value = FALSE, B = 2000)

La descripción de cada argumento se muestra a continuación:

• x: un vector numérico.
• y: para el contraste de dos muestras, es el segundo vector numérico de datos. Para el test de una muestra, una cadena de texto que contenga una función de distribución acumulada (CDF). ("pnorm", "punif", "pexp", …).
• alternative: la hipótesis alternativa. Los posibles valores son "two.sided" (por defecto), "less" (la CDF de x es menor que la CDF de y) y "greater" (la CDF de x es mayor que la CDF de y).
• exact: si se calculan p-valores exactos o no. Las posibles opciones son TRUE, FALSE y NULL (por defecto, que calcula p-valores exactos en algunos escenarios).
• simulate.p.value: si TRUE calcula los p-valores mediante simulación Monte Carlo. Por defecto es FALSE.
• B: número de réplicas de la simulación Monte Carlo. Por defecto es 2000.

Contraste para una muestra

El test de Kolmogorov-Smirnov (KS) de una muestra es un método estadístico no paramétrico utilizado para determinar si una única muestra de datos sigue una distribución continua especifica (por ejemplo, normal, exponencial, etc.) o si difiere significativamente de dicha distribución.

Sea F una distribución continua, las hipótesis nula y alternativa para la prueba de Kolmogorov-Smirnov para una sola muestra son las siguientes:

• \(H_0\): la distribución de una población ES F.
• \(H_1\): la distribución de una población NO ES F.

En el siguiente ejemplo comparamos la función de distribución empírica de una variable denominada x con la función de distribución acumulativa teórica de la distribución normal estándar. El objetivo es comprobar si la distribución de la población es normal.

# Datos de muestra
set.seed(27)
x <- rnorm(50)

# Grid de valores
grid <- seq(-4, 4, length.out = 100)

# Gráfico de las CDFs
plot(grid, pnorm(grid, mean = 0, sd = 1), type = "l",
     ylim = c(0, 1), ylab = "", lwd = 2, col = "red", xlab = "", main = "ECDFs")
lines(ecdf(x), verticals = TRUE, do.points = FALSE, col.01line = NULL)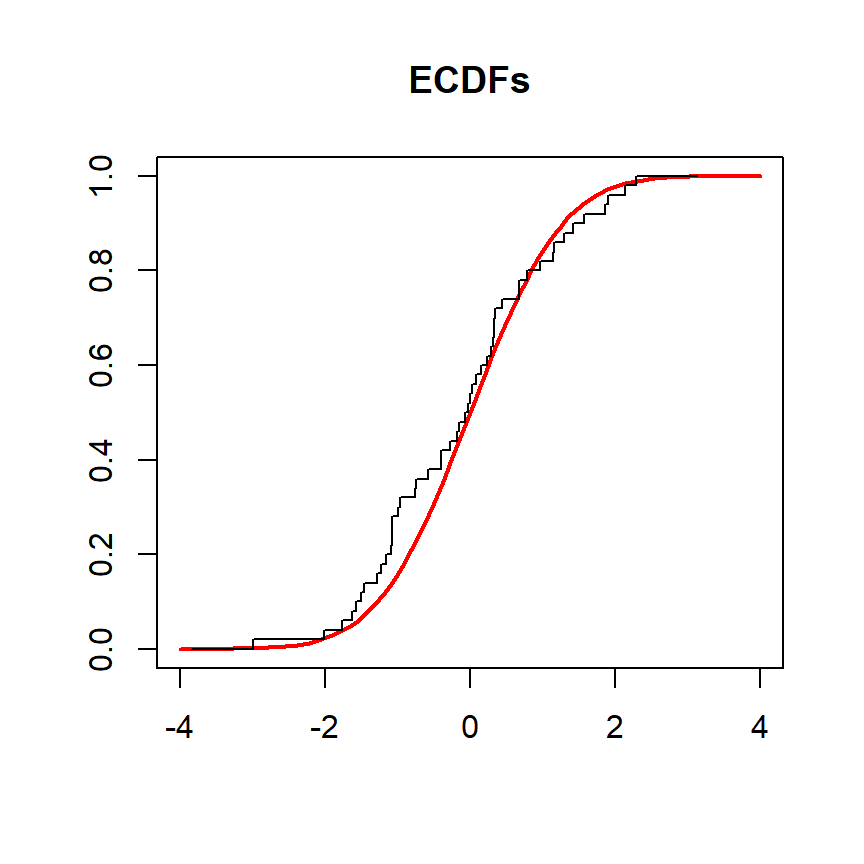

Para realizar el test tendrás que introducir los datos y el nombre de la función de distribución acumulada (como pnorm para distribución normal, punif para distribución uniforme, pexp para distribución exponencial, …) y los parámetros deseados de la distribución.

# Datos de muestra que siguen una distribución normal
set.seed(27)
x <- rnorm(50)

# ¿Proviene 'x' de una distribución normal estándar?
ks.test(x, "pnorm", mean = 0, sd = 1)

	Exact one-sample Kolmogorov-Smirnov test

data:  x
D = 0.083818, p-value = 0.8449
alternative hypothesis: two-sided

El test anterior arroja un p-valor de 0.8449, superior a los niveles de significación habituales, lo que implica que no hay pruebas para rechazar la hipótesis nula de que la distribución de los datos es normal.

Ahora, realizaremos la prueba de nuevo, pero tendremos una variable llamada y extraída de una distribución normal para ser contrastada contra una distribución uniforme en el intervalo (-4, 4). En este escenario las funciones de distribución acumulada son las siguientes:

# Datos de muestra
set.seed(27)
y <- rnorm(50)

# Grid de valores
grid <- seq(-5, 5, length.out = 100)

# Gráfico de las CDFs
plot(grid, punif(grid, min = -4, max = 4), type = "l",
     ylim = c(0, 1), ylab = "", lwd = 2, col = "red", xlab = "", main = "ECDFs")
lines(ecdf(y), verticals = TRUE, do.points = FALSE, col.01line = NULL)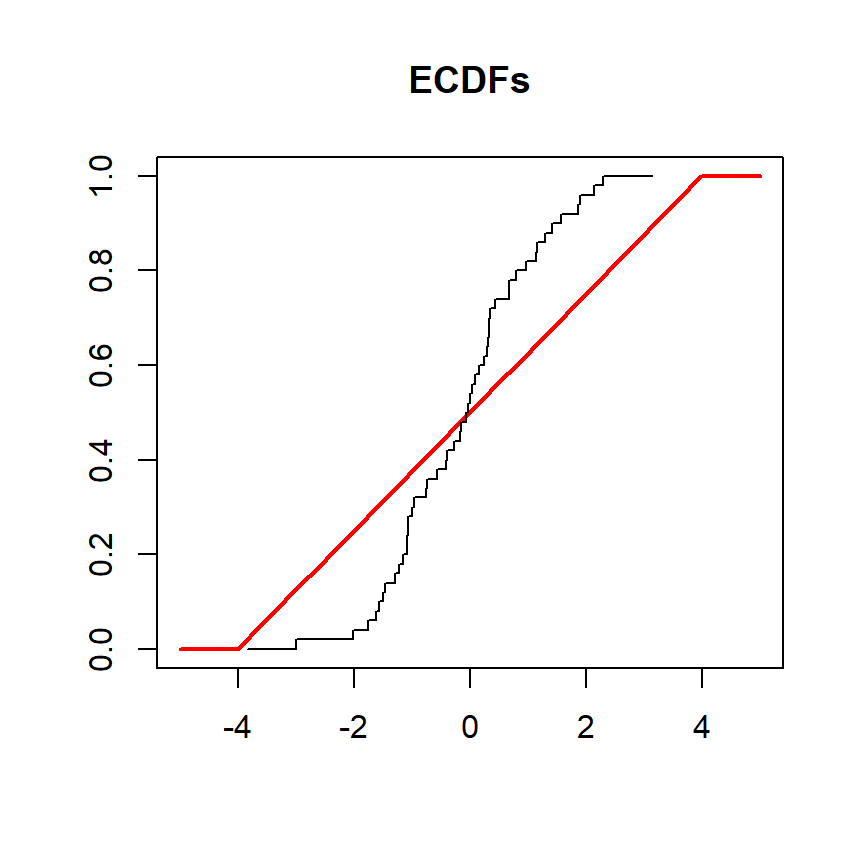

La prueba puede realizarse como se muestra en el siguiente ejemplo:

# Datos de muestra que siguen una distribución normal
set.seed(27)
y <- rnorm(50)

# ¿Proviene 'y' de una distribución uniforme en el intervalo (-4, 4)?
ks.test(y, "punif", min = -4, max = 4)

	Exact one-sample Kolmogorov-Smirnov test

data:  y
D = 0.23968, p-value = 0.005178
alternative hypothesis: two-sided

El test devuelve un p-valor cercano a cero, lo que significa que hay pruebas estadísticas para rechazar la hipótesis nula de que los datos siguen una distribución uniforme.

Contraste para dos muestras

El test de Kolmogorov-Smirnov (KS) para dos muestras es un método no paramétrico utilizado para comparar las funciones de distribución acumulada empírica de dos muestras independientes para determinar si proceden de la misma distribución subyacente.

Sean X e Y dos variables aleatorias independientes las hipótesis nula y alternativa son las siguientes:

• \(H_0\): la distribución de X ES IGUAL a la distribución de Y.
• \(H_1\): la distribución de X ES DIFERENTE a la distribución de Y.

El siguiente bloque de código ilustra cómo representar las funciones de distribución acumulada de dos variables llamadas x y y:

# Datos de muestra
set.seed(27)
x <- runif(50, min = -1, max = 1)
y <- runif(50, min = -1, max = 1)

# Gráfico de las CDFs
plot(ecdf(x), verticals = TRUE, do.points = FALSE, col.01line = NULL, xlab = "", main = "ECDFs")
lines(ecdf(y), verticals = TRUE, do.points = FALSE, col.01line = NULL, col = 4)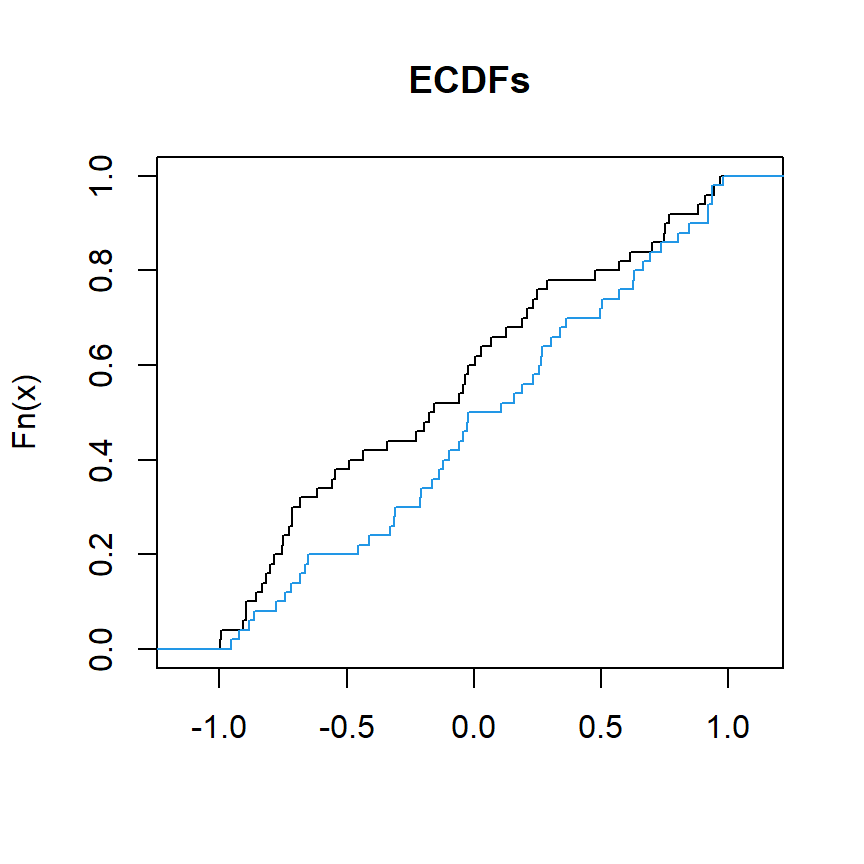

Podemos utilizar ks.test para comparar x e y y evaluar si proceden de la misma distribución.

# Datos de muestra que siguen una distribución uniforme
set.seed(27)
x <- runif(50, min = -1, max = 1)
y <- runif(50, min = -1, max = 1)

# Test de dos muestras de Kolmogorov-Smirnov
# ¿'x' e 'y' tienen la misma distribución?
ks.test(x, y)

	Asymptotic two-sample Kolmogorov-Smirnov test

data:  x and y
D = 0.2, p-value = 0.2719
alternative hypothesis: two-sided

El p-valor es 0.2719, superior a los niveles de significación habituales, por lo que no hay pruebas para rechazar la hipótesis nula. Esto significa que no hay pruebas estadísticas suficientes para concluir que las distribuciones de las dos muestras (x e y) son significativamente diferentes entre sí.