INICIO

Distribución uniforme continua en R

Estadística con R Distribuciones

La distribución uniforme es una distribución continua donde todos los intervalos de la misma longitud en el rango de la distribución acumulan la misma probabilidad. En este tutorial explicaremos cómo usar las funciones dunif, punif, qunif y runif para calcular la densidad, distribución acumulada, los cuantiles y generar observaciones aleatorias, respectivamente, de una distribución uniforme en R.

La distribución uniforme

Sea \(X \sim U(a, b)\), es decir, una variable aleatoria con distribución uniforme en el intervalo \((a, b)\), con \(a, b \in \mathbb{R}, a < b\):

La función de densidad de probabilidad (o PDF, por sus siglas en inglés) de \(x\) es \(f(x) = \frac{1}{b - a}\) si \(x \in (a, b)\) y \(0\) en otro caso.
La función de distribución acumulada (CDF) es \(F(x) = P(X \leq x) = \frac{x-a}{b-a}\).
La función cuantil es \(Q(p) = F^{-1}(p)\).
La esperanza y la varianza de \(X\) son \(E(X) = \frac{a + b}{2}\) y \(Var(X) = \frac{(b-a)^2}{12}\), respectivamente.

Las diferentes funciones de la distribución uniforme se pueden calcular en R para cualquier valor de \(x\). Estas funciones son: dunif, para la función de densidad, punif, para la distribución acumulada y qunif, para la función cuantil. Además, la función runif permite obtener \(n\) observaciones aleatorias de una distribución uniforme. Estas funciones se describen a continuación:

Función	Descripción
dunif	Densidad uniforme continua (Función de densidad de probabilidad)
punif	Distribución uniforme continua (Función de distribución)
qunif	Función cuantil de la distribución uniforme
runif	Generación de números peudoaleatorios de la distribución uniforme continua

Por defecto, estas funciones consideran la distribución uniforme en el intervalo (0, 1), también conocida como distribución uniforme estándar.

La función dunif

Para calcular la función de densidad uniforme en R en el intervalo \((a, b)\) para cualquier valor de \(x\) se puede utilizar la función dunif, que tiene la siguiente sintaxis:

dunif(x,           # Valores del eje X (rejilla de valores)
      min = 0,     # Límite inferior de la distribución (a)
      max = 1,     # Límite superior de la distribución (b)
      log = FALSE) # Si TRUE, las probabilidades se devuelven como log

Considera que quieras calcular la función de densidad de probabilidad uniforme en el intervalo \((1, 3)\) para una rejilla de valores. Con tal propósito puedes escribir:

x <- 0:4 # Rejilla
dunif(x, min = 1, max = 3)

0.0 0.5 0.5 0.5 0.0

Dibujar la función de densidad uniforme en R

Puedes crear un gráfico de la función de densidad de probabilidad e una distribución uniforme con la siguiente función:

# x: rejilla de valores del eje X (opcional)
# min: límite inferior de la distribución (a)
# max: límite superior de la distribución (b)
# lwd: ancho de los segmentos del gráfico
# col: color de los segmentos y de los puntos del gráfico
# ...: argumentos adicionales a ser pasados a la función plot
plotunif <- function(x, min = 0, max = 1, lwd = 1, col = 1, ...) {

    # Rejilla de valores del eje X
    if (missing(x)) {
        x <- seq(min - 0.5, max + 0.5, 0.01)
    }

    if(max < min) {
        stop("'min' must be lower than 'max'")
    }
   
    plot(x, dunif(x, min = min, max = max),
         xlim = c(min - 0.25, max + 0.25), type = "l",
         lty = 0, ylab = "f(x)", ...) 
    segments(min, 1/(max - min), max, 1/(max - min), col = col, lwd = lwd)
    segments(min - 2, 0, min, 0, lwd = lwd, col = col)
    segments(max, 0, max + 2, 0, lwd = lwd, col = col)
    points(min, 1/(max - min), pch = 19, col = col)
    points(max, 1/(max - min), pch = 19, col = col)
    segments(min, 0, min, 1/(max - min), lty = 2, col = col, lwd = lwd)
    segments(max, 0, max, 1/(max - min), lty = 2, col = col, lwd = lwd)
    points(0, min, pch = 21, col = col, bg = "white")
    points(max, min, pch = 21, col = col, bg = "white")
}

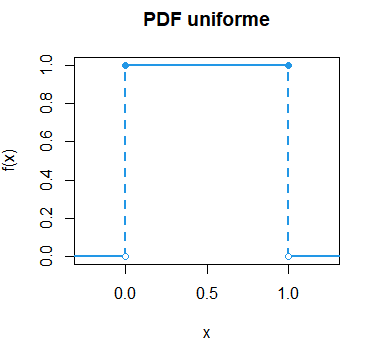
Como ejemplo, si quieres dibujar la función de densidad uniforme estándar en color azul puedes escribir:

plotunif(min = 0, max = 1, lwd = 2, col = 4, main = "PDF uniforme")

Dibujar la función de densidad uniforme en R

La función punif

En R, puedes hacer uso de la función punif para calcular la función de distribución acumulada uniforme, esto es, la probabilidad de que una variable \(X\) tome valores menores o iguales a \(x\). Esta función tiene la siguiente sintaxis:

punif(q,                  # Vector de cuantiles
      min = 0,            # Límite inferior de la distribución (a)
      max = 0,            # Límite superior de la distribución (b)
      lower.tail = TRUE,  # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
      log.p = FALSE)      # Si TRUE, las probabilidades se devuelven como log

Como ejemplo, si quieres calcular la probabilidad de que una variable en el intervalo \((0, 1)\) tome valores menores o iguales que 0.6 es:

punif(0.6) # 0.6

Ejemplo con la función punif

Veamos un caso en mayor detalle. Considera que \(X\) es el tiempo (en minutos) que una persona tiene que esperar para tomar un vuelo. Si un vuelo despega cada hora \(X \sim U(0, 60)\). Tomando lo anterior en cuenta:

La probabilidad de esperar menos de 15 minutos es \(P(X < 15) = P(X <= 15)\):

punif(15, min = 0, max = 60) # 0.25 o 25%
1 - punif(15, min = 0, max = 60, lower.tail = FALSE) # Equivalente

Hemos desarrollado la siguiente función para sombrear el área en un intervalo de la función de densidad de probabilidad uniforme con una sola línea de código:

# min: límite inferior de la distribución (a)
# max: límite superior de la distribución (b)
# lb: límite inferior del área
# ub: límite superior del área
# col: color de las líneas y puntos
# acolor: color del área
# ...: argumentos adicionales a ser pasados a la función plot
unif_area <- function(min = 0, max = 1, lb, ub, col = 1,
                      acolor = "lightgray", ...) {
    x <- seq(min - 0.25 * max, max + 0.25 * max, 0.001) 
    
    if (missing(lb)) {
       lb <- min(x)
    }
    if (missing(ub)) {
        ub <- max(x)
    }
    if(max < min) {
        stop("'min' must be lower than 'max'")
    }

    x2 <- seq(lb, ub, length = 1000) 
    plot(x, dunif(x, min = min, max = max),
         xlim = c(min - 0.25 * max, max + 0.25 * max), type = "l",
         ylab = "f(x)", lty = 0, ...)   

    y <- dunif(x2, min = min, max = max)
    polygon(c(lb, x2, ub), c(0, y, 0), col = acolor, lty = 0)
    segments(min, 1/(max - min), max, 1/(max - min), lwd = 2, col = col)
    segments(min - 2 * max, 0, min, 0, lwd = 2, col = col)
    segments(max, 0, max + 2 * max, 0, lwd = 2, col = col)
    points(min, 1/(max - min), pch = 19, col = col)
    points(max, 1/(max - min), pch = 19, col = col)
    segments(min, 0, min, 1/(max - min), lty = 2, col = col, lwd = 2)
    segments(max, 0, max, 1/(max - min), lty = 2, col = col, lwd = 2)
    points(0, min, pch = 21, col = col, bg = "white")
    points(max, min, pch = 21, col = col, bg = "white")
}

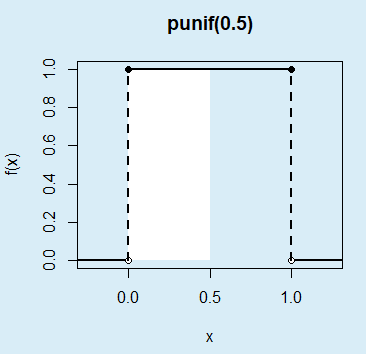
A modo ilustrativo, si quieres dibujar el área entre 0 y 0.5 de una distribución uniforme en el intervalo \((0, 1)\), que se puede calcular con punif(0.5) puedes escribir:

unif_area(min = 0, max = 1, lb = 0, ub = 0.5,
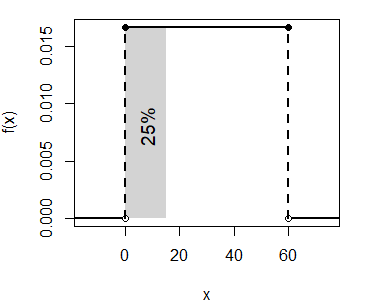
          main = "punif(0.5)", acolor = "white")

Sombrear el área de la densidad uniforme en R

La probabilidad calculada (0.25) corresponde al área:

unif_area(min = 0, max = 60, lb = 0, ub = 15)
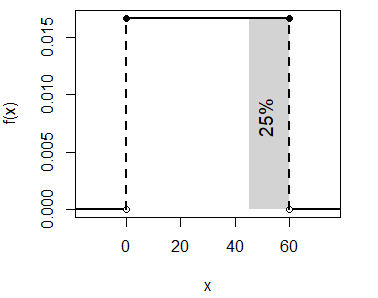
text(8, 0.008, "25%", srt = 90, cex = 1.2)

Ejemplo con la función punif en R

La probabilidad de esperar más de 45 minutos por el vuelo es \(P(X > 45) = 1 - P(X \leq 45)\):

punif(45, min = 0, max = 60, lower.tail = FALSE) # 0.25 o 25%
1 - punif(45, min = 0, max = 60) # Equivalente

Que corresponde a:

unif_area(min = 0, max = 60, lb = 45, ub = 60)
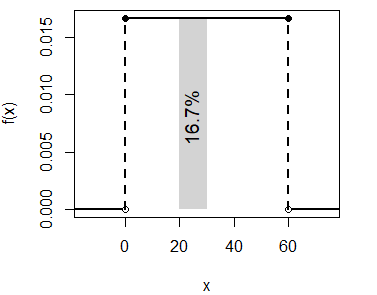
text(51, 0.008, "25%", srt = 90, cex = 1.2)

Calcular la probabilidad bajo la densidad uniforme

La probabilidad de esperar entre 20 y 30 minutos a tomar el avión es \(P(X <= 30) - P(X <= 20)\):

punif(30, min = 0, max = 60) - punif(20, min = 0, max = 60) # 0.167 o 16.7%

La probabilidad calculada se puede representar con el siguiente gráfico:

unif_area(min = 0, max = 60, lb = 20, ub = 30)
text(24, 0.008, "16.7%", srt = 90, cex = 1.2)

Probabilidad uniforme con la función punif

Como la distribución uniforme es continua \(P(X = x) = 0\), entonces \(P(X \geq x) = P(X > x)\) y \(P(X \leq x) = P(X < x)\).

Dibujar la función de distribución
acumulada en R

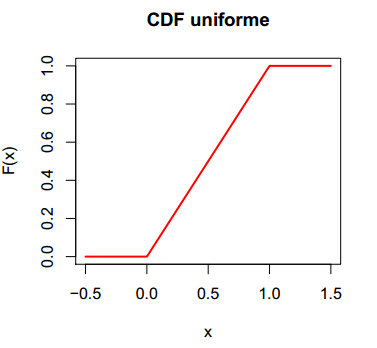
También puedes crear el gráfico de la función de distribución acumulada de la distribución uniforme en R. Para ello tienes que escribir lo siguiente:

# Rejilla de valores del eje X
x <- seq(-0.5, 1.5, 0.01)

# Distribución uniforme entre 0 y 1
plot(x, punif(x, min = 0, max = 0), type = "l", main = "CDF uniforme",
     ylab = "F(x)", lwd = 2, col = "red")

# Equivalente a:
plot(punif, -0.5, 1.5, type = "l", main = "CDF uniforme",
     ylab = "F(x)", lwd = 2, col = "red")

Gráfico de la función de distribución acumulada uniforme

La función qunif

En R, puedes calcular el cuantil correspondiente para una probabilidad (p) de una distribución uniforme con la función qunif, que tiene la siguiente sintaxis:

qunif(p,                 # Vector de probabilidades
      min = 0,           # Límite inferior de la distribución (a)
      max = 1,           # Límite superior de la distribución (b)
      lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
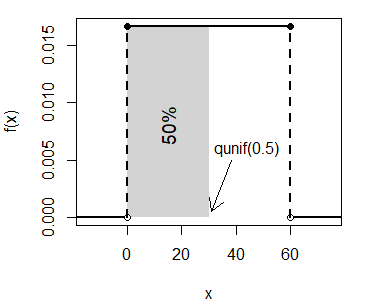
      log.p = FALSE)     # Si TRUE, las probabilidades se devuelven como log

En caso de que quieres calcular el cuantil para la probabilidad 0.5 de una distribución en el intervalo \((0, 60)\) puedes escribir:

qunif(0.5, min = 0, max = 60) # 30

unif_area(min = 0, max = 60, lb = 0, ub = 30)
text(15, 0.008, "50%", srt = 90, cex = 1.2)
arrows(38, 0.005, 31, 0.0005, length = 0.15)
text(44, 0.006, "qunif(0.5)")

Cuantil uniforme en R con la función qunif

Gráfico de la función cuantil uniforme

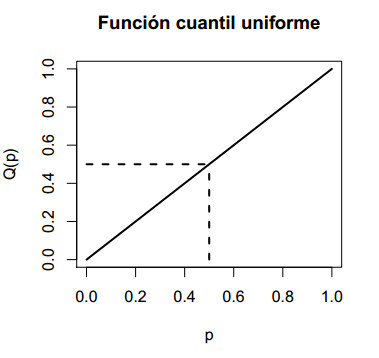
Es posible crear el gráfico de la función cuantil uniforme en R. Para ello puedes escribir lo siguiente para dibujar la función en el intervalo \((0, 1)\):

plot(qunif, punif(0), punif(1), lwd = 2,
     main = "Función cuantil uniforme",
     xlab = "p", ylab = "Q(p)")
segments(0, 0.5, punif(0.5), 0.5, lty = 2, lwd = 2)
segments(punif(0.5), 0, punif(0.5), qunif(0.5), lty = 2, lwd = 2)

Gráfico de la función cuantil uniforme

Recuerda que punif(0.5) = 0.5 y qunif(0.5) = 0.5.

La función runif

La función runif permite obtener \(n\) observaciones aleatorias de una distribución uniforme. Los argumentos de la función se describen a continuación:

runif(n        # Número de observaciones a ser generadas
      min = 0, # Límite inferior de la distribución (a)
      max = 0) # Límite superior de la distribución (b)

Como ejemplo, puedes obtener diez observaciones de una distribución uniforme en el intervalo\((-1, 1)\) escribiendo:

runif(n = 10, min = -1, max = 1)

-0.20757312 -0.46819001 -0.80643735 -0.92675885  0.80520074
 0.39716130 -0.39939392  0.78837145  0.28130687  0.09807602

Sin embargo, cada vez que ejecutes el código anterior obtendrás diez números distintos. Si quieres que la salida sea reproducible puedes fijar una semilla con la función set.seed.

set.seed(1)
runif(n = 10, min = -1, max = 1)

-0.4689827 -0.2557522  0.1457067  0.8164156 -0.5966361
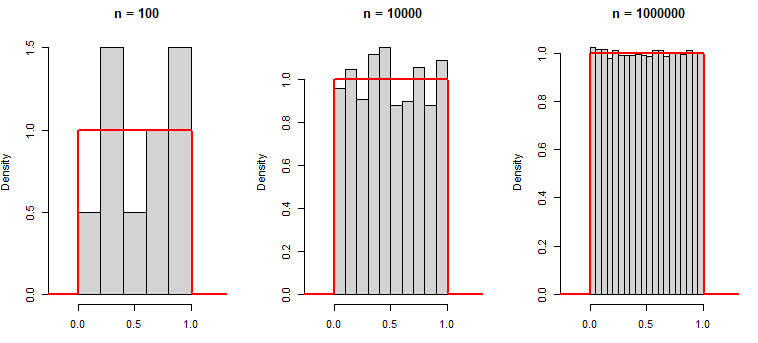
 0.7967794  0.8893505  0.3215956  0.2582281 -0.8764275

Observa que a medida que se incrementa el número de observaciones generadas, el histograma de dichas observaciones se aproxima a la función de densidad uniforme real:

# Una fila, tres columnas
par(mfrow = c(1, 3))

x <- seq(-0.5, 1.5, 0.01)

set.seed(1)

# n = 10
hist(runif(10), main = "n = 100", xlim = c(-0.2, 1.25),
     xlab = "", prob = TRUE)
lines(x, dunif(x), col = "red", lwd = 2)

# n = 1000
hist(runif(1000), main = "n = 10000", xlim = c(-0.2, 1.25),
     xlab = "", prob = TRUE)
lines(x, dunif(x), col = "red", lwd = 2)

# n = 100000
hist(runif(100000), main = "n = 1000000", xlim = c(-0.2, 1.25),
     xlab = "", prob = TRUE)
lines(x, dunif(x), col = "red", lwd = 2)

# Volvemos a una fila y una columna
par(mfrow = c(1, 1))

Generación de datos uniformes en R