Distribución de Poisson en R
La distribución de Poisson es una distribución discreta que cuenta el número de eventos en un proceso de Poisson. En este tutorial revisaremos las funciones dpois, ppois, qpois y rpois para trabajar con la distribución de Poisson en R.
La distribución de Poisson
Un proceso de Poisson es un experimento aleatorio que consiste en observar la ocurrencia de eventos específicos sobre un soporte continuo (generalmente el espacio o el tiempo), tal que el proceso es estable (el número de ocurrencias, \(\lambda\) es constante a largo plazo) y los eventos ocurren de forma aleatoria e independiente.
La distribución de Poisson se usa para modelar el número de eventos que ocurren en un proceso de Poisson. Sea \(X \sim P(\lambda)\), esto es, una variable aleatoria con distribución de Poisson donde el número medio de eventos que ocurren en un determinado intervalo es \(\lambda\):
- La función de masa de probabilidad (o PMF, por sus siglas en inglés) es \(P(X = x) =\frac{e^{- \lambda} \lambda^x}{x!}\) para \(x = 0, 1, 2, \dots\).
- La función de distribución (o CDF, por sus siglas en inglés) es \(F(x) =\sum_{i = 0}^x \frac{e ^{- \lambda} \lambda^i}{i!}\).
- La función cuantil es \(Q(p) = F ^{-1}(p)\).
- La esperanza y varianza de \(X\) son \(E(X) = Var(X) = \lambda\).
Las funciones descritas en la lista enterior se pueden calcular en R para un conjunto de valores con las funciones dpois (masa de probabilidad), ppois (distribución) y qpois (cuantil). Además, la función rpois permite obtener \(n\) observaciones aleatorias que siguen una distribución de Poisson. La tabla de abajo describe brevemente cada una de estas funciones.
| Función | Descripción |
|---|---|
| dpois |
Función de masa de probabilidad de la distribución de Poisson |
| ppois |
Función de distribución acumulada de la distribución de Poisson |
| qpois |
Función cuantil de la distribución de Poisson |
| rpois |
Generación de números pseudoaleatorios de la distribución de Poisson |
La función dpois
La función de masa de probabilidad de una distribución de Poisson de media \(\lambda\) se puede calcular en R con la función dpois para cualquier valor de \(x\). El siguiente bloque de código resume los argumentos de la función:
dpois(x, # Valores del eje X (x = 0, 1, 2, ...)
lambda, # Número medio de eventos que ocurren en el intervalo
log = FALSE) # Si TRUE, las probabilidades se devuelven como logComo ejemplo, si quieres calcular la función de masa de probabilidad de una distribución de Poisson con media 5 para \(x \in \{0, 1, \dots, 10\}\), puedes escribir:
dpois(0:10, lambda = 5)0.006737947 0.033689735 0.084224337 0.140373896 0.175467370 0.175467370
0.146222808 0.104444863 0.065278039 0.036265577 0.018132789También puedes especificar un vector de medias en lugar de un único valor, como en el siguiente bloque de código:
dpois(5, lambda = c(5, 10)) # 0.17546737 0.03783327En el ejemplo anterior, el primer elemento de la salida procede de una distribución con media \(\lambda = 5\) y el segundo de una distribución con media \(\lambda = 10\) eventos por intervalo.
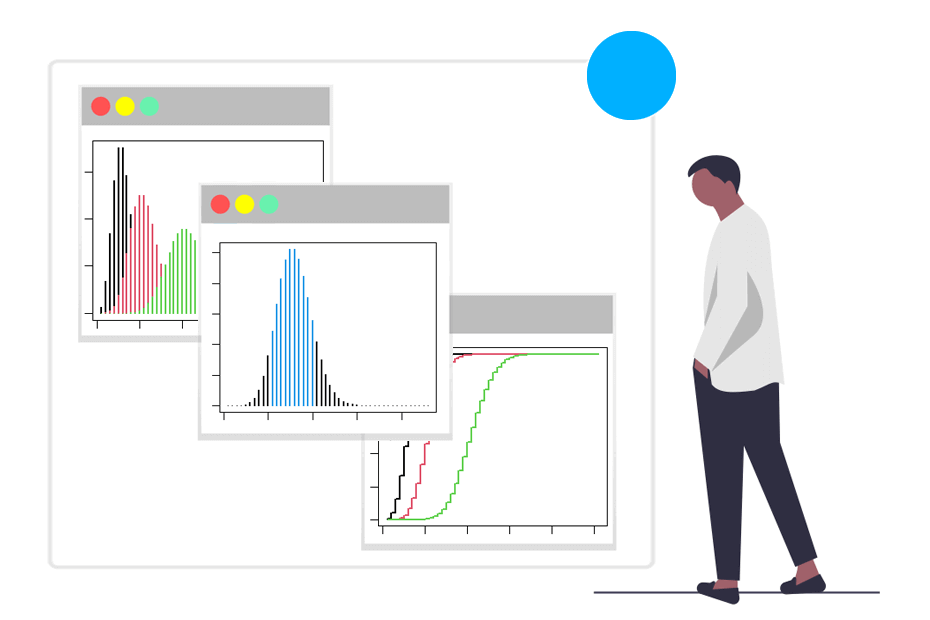
Gráfico de la función de probabilidad de la distribución de Poisson en R
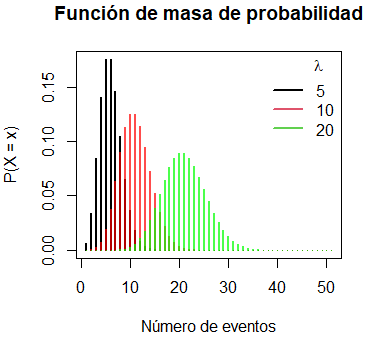
La función de masa de probabilidad de la Poisson se puede dibujar en R haciendo uso de la función plot, como en el siguiente ejemplo:
# Rejilla de valores del eje X
x <- 0:50
#-----------
# lambda: 5
#-----------
lambda <- 5
plot(dpois(x, lambda), type = "h", lwd = 2,
main = "Función de masa de probabilidad",
ylab = "P(X = x)", xlab = "Número de eventos")
#-----------
# lambda: 10
#-----------
lambda <- 10
lines(dpois(x, lambda), type = "h", lwd = 2, col = rgb(1,0,0, 0.7))
#-----------
# lambda: 20
#-----------
lambda <- 20
lines(dpois(x, lambda), type = "h", lwd = 2, col = rgb(0, 1, 0, 0.7))
# Leyenda
legend("topright", legend = c("5", "10", "20"),
title = expression(lambda), title.adj = 0.75,
lty = 1, col = 1:3, lwd = 2, box.lty = 0)La función ppois
La probabilidad de que una variable \(X\) siguiendo una distribución de Poisson tome valores menores o iguales a \(x\) se puede calcular con la función ppois, cuyos argumentos se describen a continuación:
ppois(q, # Cuantil o vector de cuantiles
lambda, # Media o vector de medias
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
log.p = FALSE) # Si TRUE, las probabilidades se devuelven como logSi quieres calcular, por ejemplo, la probabilidad de observar 5 o menos eventos \((P(X \leq 5))\) si la media de ocurrencia de los eventos en un intervalo específico es 10 puedes escribir:
ppois(5, lambda = 10) # 0.06708596En este ejemplo, el anterior resultado es equivalente a la suma de las probabilidades de cada valor hasta 5:
sum(dpois(0:5, lambda = 10)) # 0.06708596Ejemplo con la función ppois
En esta sección vamos a presentar un ejemplo en detalle usando la función ppois. Considera que el número de visitas a una página web sigue una distribución de Poisson con media 15 visitas por hora. Por tanto, \(\lambda = 15\).
- La probabilidad de obtener 10 visitas o menos por hora, \(P(X \leq 10)\), es:
ppois(10, lambda = 15) # 0.1184644 o 11.8%
1 - ppois(10, lambda = 15, lower.tail = FALSE) # Equivalente
sum(dpois(0:10, lambda = 15)) # EquivalenteComo la distribución de Poisson es discreta, la probabilidad acumulada se calcula sumando las correspondientes probabilidades de la función de masa de probabilidad. La siguiente función de R permite visualizar las probabilidades que se suman basadas en un límite inferior y uno superior.
# lambda: media
# lb: límite inferior de la suma
# ub: límite supeior de la suma
# col: color
# lwd: ancho de línea
pois_sum <- function(lambda, lb, ub, col = 4, lwd = 1, ...) {
x <- 0:(lambda + lambda * 2)
if (missing(lb)) {
lb <- min(x)
}
if (missing(ub)) {
ub <- max(x)
}
plot(dpois(x, lambda = lambda), type = "h", lwd = lwd, ...)
if(lb == min(x) & ub == max(x)) {
color <- col
} else {
color <- rep(1, length(x))
color[(lb + 1):ub ] <- col
}
lines(dpois(x, lambda = lambda), type = "h",
col = color, lwd = lwd, ...)
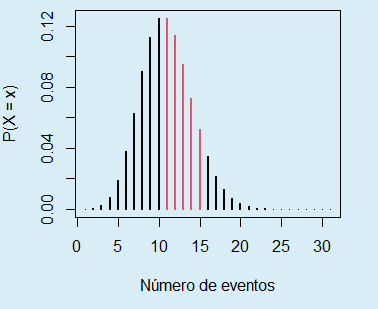
}A modo ilustrativo, si quieres mostrar las probabilidades que se van a sumar para calcular la probabilidad de observar entre 10 y 15 eventos, si ocurren 10 eventos de media en cada intervalo, puedes escribir:
pois_sum(lambda = 10, lb = 10, ub = 15, lwd = 2,
col = 2, ylab = "P(X = x)", xlab = "Número de eventos")La suma de las probabilidades mostradas en rojo es igual a ppois(15, lambda = 10) - ppois(10, lambda = 10).
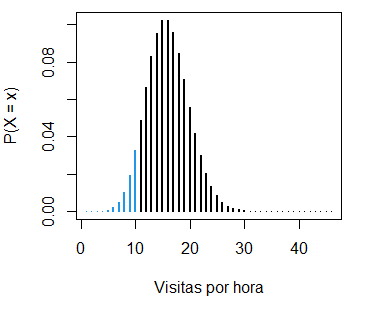
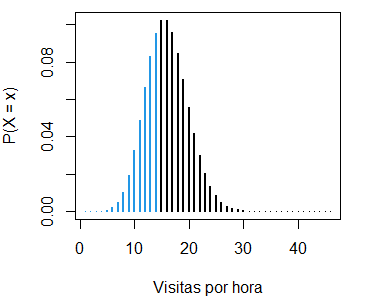
La probabilidad calculada (11.8%) corresponde a la suma de las siguientes probabilidades:
pois_sum(lambda = 15, ub = 10, lwd = 2,
ylab = "P(X = x)", xlab = "Visitas por hora")- La probabilidad de obtener más de 20 visitas por hora, \(P(X > 20)\), es:
ppois(20, lambda = 15, lower.tail = FALSE) # 0.08297091 o 8.3%
1 - ppois(20, lambda = 15) # Equivalente
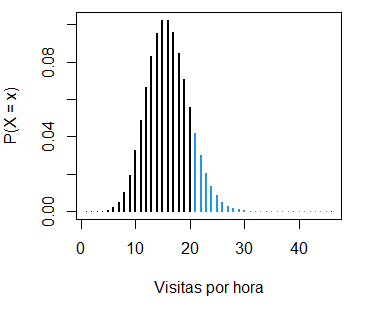
1 - sum(dpois(0:20, lambda = 15)) # EquivalenteEsta probabilidad corresponde a:
pois_sum(lambda = 15, lb = 20, lwd = 2,
ylab = "P(X = x)", xlab = "Visitas por hora")- La probabilidad de recibir menos de 15 visitas por hora, \(P(X < 15)\) es:
ppois(14, lambda = 15, lower.tail = FALSE) # 0.5343463 o 53.43%
1 - sum(dpois(0:15, lambda = 15)) # EquivalenteTen en cuenta que establecemos 14 en lugar de 15 porque la distribución de Poisson es discreta, por lo que \(P(X < 15) = P(X \leq 14)\). El gráfico correspondiente es como sigue:
pois_sum(lambda = 15, ub = 14, lwd = 2,
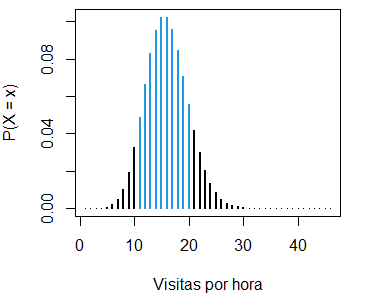
ylab = "P(X = x)", xlab = "Visitas por hora")- La probabilidad de obtener entre 10 y 20 visitas por hora es:
ppois(20, lambda = 15) - ppois(10, lambda = 15) # 0.7985647 o 79.86%
sum(dpois(11:20, lambda = 15)) # EquivalenteLa probabilidad se puede representar haciendo uso de la función que definimos antes:
pois_sum(lambda = 15, lb = 10, ub = 20, lwd = 2,
ylab = "P(X = x)", xlab = "Visitas por hora")Como la distribución de Poisson es una distribución discreta \(P(X = x) \neq 0\), por lo que \(P(X \geq x) \neq P(X > x)\) y \(P(X \leq x) \neq P(X < x)\).
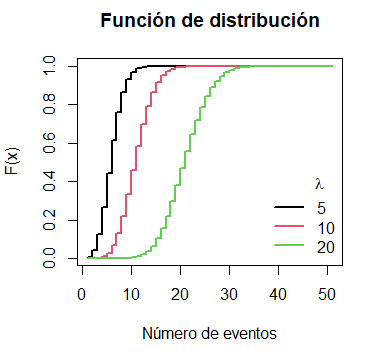
Gráfico de la función de distribución de Poisson en R
La función de distribución acumulada de una distribución de Poisson se puede representar para diferentes valores de \(\lambda\) con el siguiente bloque de código:
# Rejilla de valores del eje X
x <- 0:50
#-----------
# lambda: 5
#-----------
lambda <- 5
plot(ppois(x, lambda), type = "s", lwd = 2,
main = "Función de distribución",
xlab = "Número de eventos", ylab = "F(x)")
#-----------
# lambda: 10
#-----------
lambda <- 10
lines(ppois(x, lambda), type = "s", lwd = 2, col = 2)
#-----------
# lambda: 20
#-----------
lambda <- 20
lines(ppois(x, lambda), type = "s", lwd = 2, col = 3)
# Legend
legend("bottomright", legend = c("5", "10", "20"),
title = expression(lambda), title.adj = 0.75,
lty = 1, col = 1:3, lwd = 2, box.lty = 0)La función qpois
La función qpois permite obtener los cuantiles correspondientes de la distribución de Poisson para un conjunto de probabilidades.
qpois(p, # Probabilidad o vector de probabilidades
lambda, # Media o vector de medias
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
log.p = FALSE) # Si TRUE, las probabilidades se devuelven como logPor ejemplo, el cuantil 0.5 de una distribución de Poisson es igual a la media:
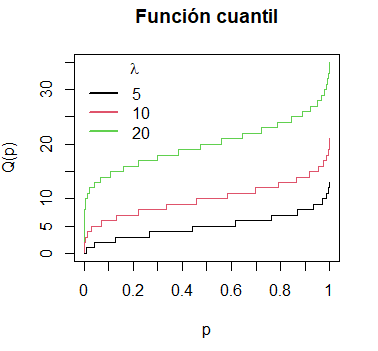
qpois(0.5, lambda = 10) # 10Gráfico de la función cuantil de la distribución de Poisson
Las funciones cuantil de la distribución de Poisson se pueden dibujar en R para un conjunto de probabilidades. El siguiente gráfico muestra los salidas de la función qpois para diferentes medias.
#-----------
# lambda: 20
#-----------
plot(qpois(seq(0, 1, 0.001), lambda = 20),
main = "Función cuantil",
ylab = "Q(p)", xlab = "p",
type = "s", col = 3, xaxt = "n")
axis(1, labels = seq(0, 1, 0.1), at = 0:10 * 100)
#-----------
# lambda: 10
#-----------
lines(qpois(seq(0, 1, 0.001), lambda = 10), type = "s", col = 2)
#-----------
# lambda: 5
#-----------
lines(qpois(seq(0, 1, 0.001), lambda = 5), type = "s")
# Legend
legend("topleft", legend = c("5", "10", "20"),
title = expression(lambda), title.adj = 0.75,
lty = 1, col = 1:3, lwd = 2, box.lty = 0)La función rpois
Si quieres obtener \(n\) observaciones de una distribución de Poisson puedes hacer uso de la función rpois. El siguiente bloque de código resume los argumentos de la función.
rpois(n, # Número de observaciones a ser generadas
lambda) # Media o vector de mediasSi quieres obtener 10 observaciones aleatorias de una distribución de Poisson con media 4 puedes escribir:
rpois(10, lambda = 4)7 6 2 2 3 6 3 4 4 7Sin embargo, la salida anterior no será reproducible. En caso de que quieras generar una secuencia reproducible de números puedes fijar una semilla con cualquier número entero de la siguiente manera:
set.seed(10)
rpois(10, lambda = 4)4 3 3 5 1 2 3 3 4 3