Distribución exponencial en R
La distribución exponencial es una distribución de probabilidad continua que se utiliza para modelar el tiempo o espacio entre eventos en un proceso de Poisson. En este tutorial aprenderás a utilizar las funciones dexp, pexp, qexp y rexp y las diferencias entre ellas. Por lo tanto, aprenderás a calcular y dibujar las funciones de densidad y distribución, calcular probabilidades, cuantiles y generar muestras aleatorias siguiendo una distribución exponencial en R.
La distribución exponencial
La distribución exponencial es la distribución de probabilidad del tiempo o espacio entre dos eventos en un proceso de Poisson, donde los eventos ocurren de manera continua e independiente a una tasa constante \(\lambda\).
Como en toda distribución, es importante conocer su función de densidad de probabilidad, su función de distribución y su función cuantil. Sea \(X \sim Exp(\lambda)\), es decir, una variable aleatoria con distribución exponencial de parámetro \(\lambda\):
- La función de densidad (o PDF, por sus siglas en inglés) de \(x\) es \(f(x) = \lambda e^{- \lambda x}\) si \(x \geq 0\) o \(0\) en otro caso.
- La función de distribución acumulada (o CDF, por sus siglas en inglés) es \(F(x) = P(X \leq x) = 1 - e^{-\lambda x}\) si \(x \geq 0\) o \(0\) en otro caso.
- La función cuantil es \(Q(p) = F^{-1}(p) = \frac{-ln (1 - p)}{\lambda}\).
- La esperanza y la varianza de \(X\) son \(E(X) = \frac{1}{\lambda}\) y \(Var(X) = \frac{1}{\lambda ^2}\), respectivamente.
En R, las las funciones anteriores se pueden calcular con las funciones dexp, pexp y qexp. Además, la función rexp permite obtener observaciones aleatorias siguiendo una distribución exponencial. Las funciones se describen en la siguiente tabla:
| Función | Descripción |
|---|---|
| dexp |
Densidad exponencial (Función de densidad de probabilidad) |
| pexp |
Distribución exponencial (Función de distribución acumulada) |
| qexp | Función cuantil de la distribución exponencial |
| rexp |
Generación de números pseudoaleatorios exponenciales |
Por defecto, estas funciones consideran la distribución exponencial con parámetro \(\lambda = 1\).
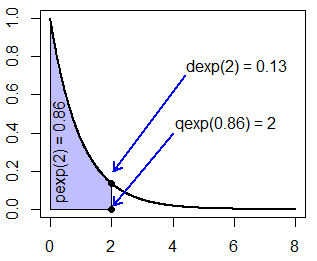
Aunque veremos cómo utilizar cada función en su correspondiente sección, puedes ver la relación entre las tres primeras funciones en el siguiente gráfico para \(\lambda = 1\):
La función dexp
La función en R para calcular la función de densidad de probabilidad exponencial de \(\lambda\) para cualquier valor de \(x\) es la función dexp, que se describe a continuación:
dexp(x, # Valores del eje X (> 0)
rate = 1, # Vector de parámetros (lambdas)
log = FALSE) # Si TRUE, las probabilidades vienen dadas como logaritmoComo ejemplo, si quieres calcular la función de densidad exponencial de parámetro 2 en R para una serie de valores, puedes escribir:
# Rejilla de valores
x <- seq(from = 0, to = 8, by = 0.01)
# PDF exponencial de parámetro lambda = 2
dexp(x, rate = 2)Sin embargo, recuerda que el parámetro no es el valor esperado, por lo tanto, si quieres calcular, por ejemplo, una distribución exponencial en R con media 10, deberás calcular el parámetro correspondiente:
# Función de densidad exponencial con media 10
dexp(x, rate = 0.1) # E(X) = 1/lambda = 1/0.1 = 10Dibujar la densidad exponencial en R
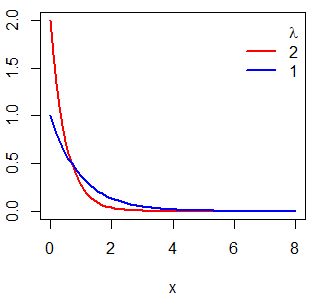
Con la salida de la función dexp puedes dibujar la densidad de una distribución exponencial. Para ello, debes pasar la rejilla del eje X como primer argumento de la función plot y la función dexp como segundo argumento. En el siguiente bloque de código mostramos cómo crear las funciones de densidad para \(\lambda = 1\) y \(\lambda = 2\).
# Rejilla del eje X
x <- seq(0, 8, 0.1)
# lambda = 2
plot(x, dexp(x, 2), type = "l",
ylab = "f(x)", lwd = 2, col = "red")
# lambda = 1
lines(x, dexp(x, rate = 1), col = "blue", lty = 1, lwd = 2)
# Agregamos una leyenda
legend("topright", c(expression(paste(, lambda)), "2", "1"),
lty = c(0, 1, 1), col = c("blue", "red"), box.lty = 0, lwd = 2)La función pexp
La función de R que permite calcular la probabilidad de que una variable aleatoria exponencial \(X\) tome valores menores o iguales que \(x\) es la función pexp, que tiene la siguiente sintaxis:
pexp(q,
rate = 1,
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
log.p = FALSE)Por ejemplo, la probabilidad de que la variable (con \(\lambda = 1\)) tome un valor menor o igual a 2 es 0.8646647:
pexp(2) # 0.8646647Ejemplo con pexp: calculando probabilidades exponenciales
Se sabe que el tiempo en una página web sigue una distribución exponencial con una media de 5 minutos por visita. En consecuencia, como \(E(X) = \frac {1}{\lambda}\); \(5 = \frac {1}{\lambda}\); \(\lambda = 0.2\).
Primero, si quieres calcular la probabilidad de que la visita dure como mucho 3 minutos, puedes escribir:
pexp(3, rate = 0.2) # 0.4511884 o 45.12%
1 - pexp(3, rate = 0.2, lower.tail = FALSE) # EquivalentePara dibujar el área bajo una curva exponencial con una sola línea de código, puedes utilizar la siguiente función que hemos desarrollado:
# rate: parámetro lambda
# lb: límite inferior del área
# ub: límite superior del área
# acolor: color del área
# ...: argumentos adicionales a ser pasados a la función lines
exp_area <- function(rate = 1, lb, ub, acolor = "lightgray", ...) {
x <- seq(0, 12/rate, 0.01)
if (missing(lb)) {
lb <- min(x)
}
if (missing(ub)) {
ub <- max(x)
}
x2 <- seq(lb, ub, length = 100)
plot(x, dexp(x, rate = rate), type = "n", ylab = "")
y <- dexp(x2, rate = rate)
polygon(c(lb, x2, ub), c(0, y, 0), col = acolor)
lines(x, dexp(x, rate = rate), type = "l", ...)
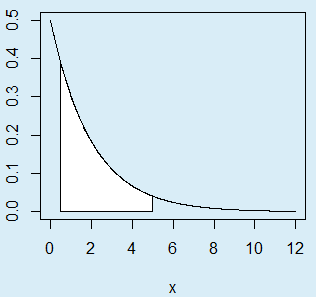
}Como ejemplo, se puede trazar el área bajo una curva exponencial de parámetro 0.5 entre 0.5 y 5 con el siguiente código:
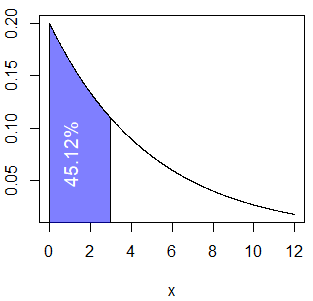
exp_area(rate = 0.5, lb = 0.5, ub = 5, acolor = "white")La probabilidad calculada (45.12%) corresponde a el área:
exp_area(rate = 0.2, ub = 3, acolor = rgb(0, 0, 1, alpha = 0.5))
text(1, 0.075, "45.12%", srt = 90, col = "white", cex = 1.2)En segundo lugar, si quieres calcular la probabilidad de que la visita dure más de 10 minutos, puedes escribir:
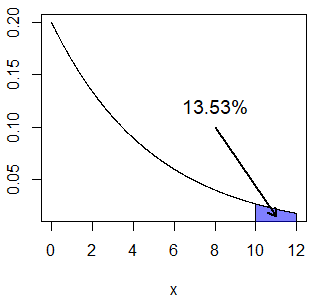
pexp(10, rate = 0.2, lower.tail = FALSE) # 0.1353353 o 13.53%El área que corresponde a la probabilidad anterior se puede dibujar con el siguiente código:
exp_area(rate = 0.2, lb = 10, acolor = rgb(0, 0, 1, alpha = 0.5))
arrows(8, 0.1, 11, 0.015, length = 0.1, lwd = 2)
text(8, 0.12, "13.53%", cex = 1.2)Finalmente, la probabilidad de que la visita dure entre 2 y 6 minutos es:
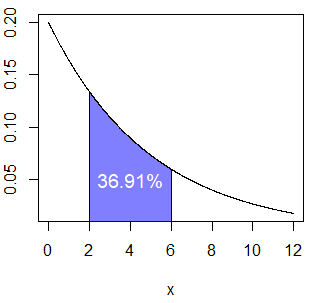
pexp(6, rate = 0.2) - pexp(2, rate = 0.2) # 0.3691258 o 36.91%El gráfico correspondiente es el que sigue:
exp_area(rate = 0.2, lb = 2, ub = 6, acolor = rgb(0, 0, 1, alpha = 0.5))
text(4, 0.05, "36.91%", col = "white", cex = 1.2)Como la distribución exponencial es una distribución continua \(P(X = x) = 0\), por lo que \(P(X \geq x) = P(X > x)\) y \(P(X \leq x) = P(X < x)\).
Gráfico de la función de distribución exponencial acumulada en R
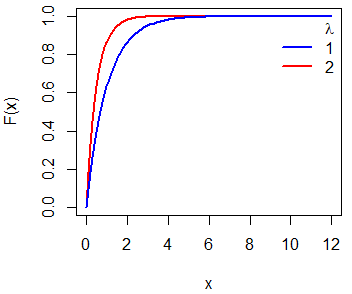
Puedes trazar la función de distribución exponencial acumulada pasando la rejilla de valores como primer argumento de la función plot y la salida de la función pexp como el segundo. Con el siguiente código dibujamos las funciones de distribución para parámetros 1 y 2.
# Rejilla de valores del eje X
x <- seq(0, 12, 0.1)
# lambda = 2
plot(x, pexp(x, 2), type = "l",
ylab = "F(x)", lwd = 2, col = "red")
# lambda = 1
lines(x, pexp(x, rate = 1), col = "blue", lty = 1, lwd = 2)
# Añadimos una leyenda
legend("topright", c(expression(paste(, lambda)), "1", "2"),
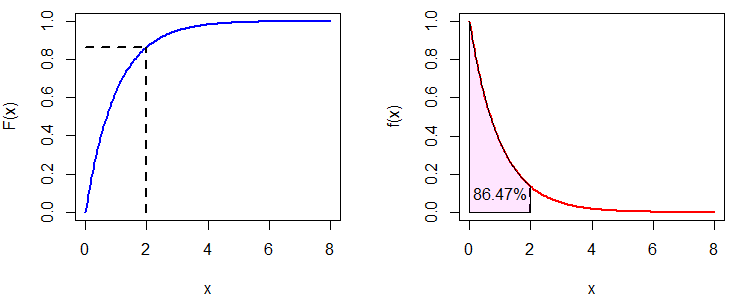
lty = c(0, 1, 1), col = c("red", "blue"), box.lty = 0, lwd = 2)Recuerda que pexp(2) era igual a 0.8646647. En el siguiente gráfico puedes ver la relación entre la distribución y la función de densidad exponencial.
par(mfrow = c(1, 2))
#-------------------------------------
# Función de distribución
#-------------------------------------
plot(x, pexp(x), type = "l", ylab = "F(x)", col = "blue", lwd = 2)
segments(2, 0, 2, pexp(2), lwd = 2, lty = 2)
segments(0, pexp(2), 2, pexp(2), lwd = 2, lty = 2)
#-------------------------------------
# Función de densidad de probabilidad
#-------------------------------------
plot(x, dexp(x), type = "l", ylab = "f(x)", col = "red", lwd = 2)
# Area
exp_area(rate = 1, ub = 2, acolor = rgb(1, 0, 1, alpha = 0.1))
# Texto
text(1, 0.1, "86.47%")La función qexp
La función qexp permite calcular el cuantil correspondiente para cualquier probabilidad \(p\):
qexp(q,
rate = 1,
lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
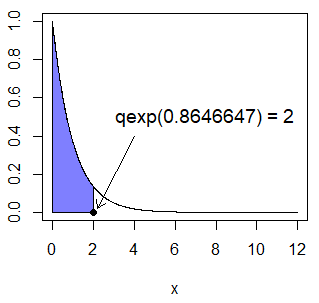
log.p = FALSE)Como ejemplo, si quieres calcular el cuantil para la probabilidad 0.8646647 (\(Q(0.86)\)) puedes escribir:
qexp(0.8646647) # 2
qexp(1 - 0.8646647, lower.tail = FALSE) # Equivalenteexp_area(rate = 1, ub = 2, acolor = rgb(0, 0, 1, alpha = 0.5))
points(2, 0, pch = 19)
arrows(4, 0.4, 2.2, 0.02, length = 0.1)
text(7.5, 0.5, "qexp(0.8646647) = 2", cex = 1.2)Recuerda que pexp(2) era 0.8646647.
Establece lower.tail = FALSE si quieres que la probabilidad esté en la cola derecha.
Dibujar la función cuantil exponencial
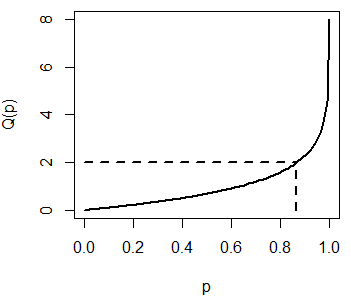
Puedes hacer un gráfico de la función cuantílica exponencial, que muestra los posibles resultados de la función qexp, con el código del siguiente bloque:
plot(qexp, pexp(0), pexp(8), lwd = 2, xlab = "p", ylab = "Q(p)")
segments(0, 2, pexp(2), 2, lty = 2, lwd = 2)
segments(pexp(2), 0, pexp(2), qexp(0.8646647), lty = 2, lwd = 2)Recuerda que pexp(2) es 0.8647 y que qexp(0.8647) es 2.
La función rexp
La función rexp permite obtener \(n\) observaciones de una distribución exponencial. La sintaxis de la función es la siguiente:
rexp(n, # Número de observaciones a ser generadas
rate = 1) Como ejemplo, si deseas extraer diez observaciones de una distribución exponencial de parámetro 1, puedes escribir:
rexp(10)Sin embargo, si quieres que la salida sea reproducible, deberás establecer una semilla para el generador de números pseudoaleatorios de R:
set.seed(1)
rexp(10)0.7551818 1.1816428 0.1457067 0.1397953 0.4360686
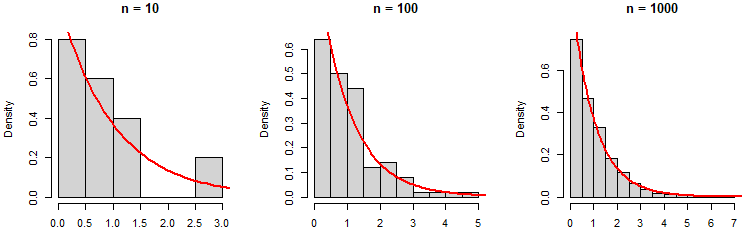
2.8949685 1.2295621 0.5396828 0.9565675 0.1470460Puedes comprobar que a medida que aumenta el número de observaciones, el histograma de los datos se aproximan a la función de densidad exponencial real:
# Dividimos la ventana gráfica en tres columnas
par(mfrow = c(1, 3))
# Rejilla de valores del eje X
x <- seq(0, 12, length = 200)
# Fijamos semilla
set.seed(1)
# n = 10
hist(rexp(10), main = "n = 10",
xlab = "", prob = TRUE)
lines(x, dexp(x), col = "red", lwd = 2)
# n = 100
hist(rexp(100), main = "n = 100",
xlab = "", prob = TRUE)
lines(x, dexp(x), col = "red", lwd = 2)
# n = 1000
hist(rexp(1000), main = "n = 1000",
xlab = "", prob = TRUE)
lines(x, dexp(x), col = "red", lwd = 2)
# Volvemos a la ventana gráfica original
par(mfrow = c(1, 1))