Distribución binomial en R

Estadística con R Distribuciones
Función de distribución binomial en R con las funciones dbinom, pbinom, qbinom y rbinom

La distribución binomial es una distribución discreta que cuenta el número de éxitos en experimentos o ensayos de Bernoulli. En este tutorial explicaremos cómo trabajar con la distribución binomial en R con las funciones dbinom, pbinom, qbinom, y rbinom, así como crear gráficos de la función de masa de probabilidad, de distribución y de la función cuantil.

La distribución binomial

Un proceso de Bernoulli es la repetición de un experimento aleatorio (un ensayo de Bernoulli) donde cada observación independiente se clasifica como éxito, si el evento ocurre, o como fracaso en otro escenario y la proporción de éxitos en la población es constante y no depende de su tamaño.

Sea \(X \sim B(n, p)\), es decir, una variable aleatoria que sigue una distribución binomal, donde \(n\) el número de ensayos de Bernoulli, \(p\) la probabilidad de éxito y \(q = 1 - p\) la probabilidad de fracaso:

  • La función de masa de probabilidad es \(P(X = x) = \binom{n}{x}p^x q^{n-x}\) si \(x = 0, 1, 2, \dots, n\).
  • La función de distribución acumulada (o CDF, por sus siglas en inglés) es \(F(x) = I_q(1 - x, n-x)\).
  • La función cuantil es \(Q(p) = F^{-1}(p)\).
  • La esperanza y la varianza de \(X\) son \(E(X) = np\) y \(Var(X) = npq\), respectivamente.

Las funciones de la lista anterior se pueden calcular en R para un conjunto de valores con las funciones dbinom (probabilidad), pbinom (distribución) y qbinom (cuantil). Además de estas tres funciones, la función rbinom permite obtener \(n\) observaciones aleatorios que siguen una distribución binomial en R. La siguiente tabla describe brevemente dichas funciones.

Función Descripción
dbinom Función de masa de probabilidad Binomial
(Función de probabilidad)
pbinom Distribución binomial
(Función de distribución acumulada)
qbinom Función cuantil binomial
rbinom Generación de números
pseudoaleatorios binomiales

En las siguientes secciones revisaremos cada una de las funciones anteriores en detalle.

La función dbinom

Para calcular la función de probabilidad binomial para un conjunto de valores, \(x\), un número de ensayos \(n\) y una probabilidad de éxito \(p\) puedes hacer uso de la función dbinom, que tiene la siguiente sintaxis:

dbinom(x,           # Valores del eje X (x = 0, 1, 2, ..., n)
       size,        # Número de ensayos (n > = 0)
       prob,        # Probabilidad de éxito en cada ensayo
       log = FALSE) # Si TRUE, las probabilidades se devuelven como log

Si quieres calcular, por ejemplo, la función de masa de probabilidad binomial para \(x = 1, 2, \dots, 10\) y probabilidad de éxito en cada ensayo de 0.2, puedes escribir:

dbinom(x = 1:10, size = 10, prob = 0.2)
0.2684354560 0.3019898880 0.2013265920 0.0880803840 0.0264241152
0.0055050240 0.0007864320 0.0000737280 0.0000040960 0.0000001024

Gráfico de la función de probabilidad binomial en R

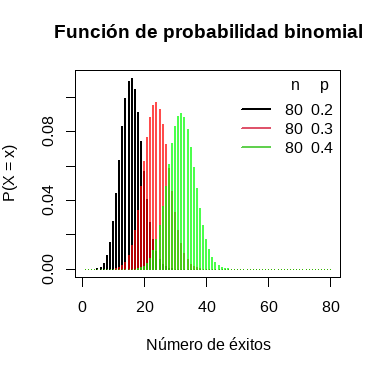
La función de masa de probabilidad binomial se puede dibujar en R haciendo uso de la función plot, pasando la salida de la función dbinom para un conjunto de valores al primer argumento de la función y estableciendo type = “h” como sigue:

# Rejilla de valores del eje X
x <- 1:80

# n = 80, p = 0.2
plot(dbinom(x, size = 80, prob = 0.2), type = "h", lwd = 2,
     main = "Función de probabilidad binomial",
     ylab = "P(X = x)", xlab = "Número de éxitos")

# n = 80, p = 0.3
lines(dbinom(x, size = 80, prob = 0.3), type = "h",
      lwd = 2, col = rgb(1,0,0, 0.7))

# n = 80, p = 0.4
lines(dbinom(x, size = 80, prob = 0.4), type = "h",
      lwd = 2, col = rgb(0, 1, 0, 0.7))

# Añadimos una leyenda
legend("topright", legend = c("80  0.2", "80  0.3", "80  0.4"),
       title = "n     p", title.adj = 0.85,
       lty = 1, col = 1:3, lwd = 2, box.lty = 0)

Función de probabilidad binomial en R

La función pbinom

Para calcular la probabilidad de que una variable \(X\) que sigue una distribución binomial tome valores menores o iguales a \(x\) puedes hacer uso de la función pbinom, cuyos argumentos se describen a continuación:

pbinom(q,                 # Cuantil o vector de cuantiles
       size,              # Número de experimentos (n > = 0)
       prob,              # Probabilidad de éxito en cada experimento
       lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
       log.p = FALSE)     # Si TRUE, las probabilidades se devuelven como log

A modo ilustrativo, la probabilidad de que el éxito ocurra menos de 3 veces si el número de ensayos es 10 y la probabilidad de éxito por ensayo es 0.3 es:

pbinom(3, size = 10, prob = 0.3) # 0.6496107 o 64.96%

Como la distribución binomial es discreta, la probabilidad anterior también puede ser calculada sumando cada valor de la función de probabilidad hasta tres.

sum(dbinom(0:3, size = 10, prob = 0.3)) # 0.6496107 o 64.96%

Como la distribución binomial es discreta, la probabilidad acumulada también se puede calcular como la suma de las correspondientes probabilidades de la función de probabilidad. La siguiente función de R permite visualizar las probabilidades que se suman basándose en un límite inferior y un límite superior de la función de probabilidad.

# size: número de ensayos (n > = 0)
# prob: probabilidad de éxito en cada ensayo
# lb: límite inferior de la suma
# ub: límite superior de la suma
# col: color
# lwd: ancho de línea
binom_sum <- function(size, prob, lb, ub, col = 4, lwd = 1, ...) {
    x <- 0:size
    
    if (missing(lb)) {
       lb <- min(x)
    }
    if (missing(ub)) {
        ub <- max(x)
    }
      
    plot(dbinom(x, size = size, prob = prob), type = "h", lwd = lwd, ...)
  
    if(lb == min(x) & ub == max(x)) {
        color <- col
    } else {
        color <- rep(1, length(x))
        color[(lb + 1):ub ] <- col
    }
    
    lines(dbinom(x, size = size, prob = prob), type = "h",
          col =  color, lwd = lwd, ...)
}

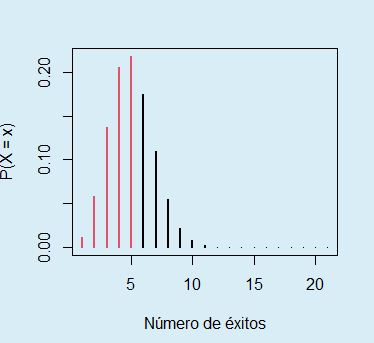
Como ejemplo, puedes representar las probabilidades que van a ser sumadas para calcular la probabilidad de que una variable binomial tome valores menores o iguales que 5 si el número de ensayos es 20 y la probabilidad de éxito es 0.2 con el siguiente código:

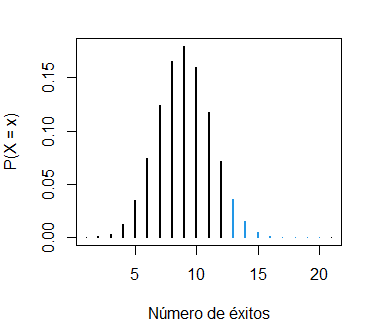
binom_sum(size = 20, prob = 0.2, lwd = 2, col = 2, ub = 5,
          ylab = "P(X = x)", xlab = "Número de éxitos")

Gráfico que muestra las probabilidades que van a ser sumadas para calcular pbinom

La suma de las probabilidades mostradas en rojo es igual a pbinom(5, size = 20, prob = 0.2).

Ejemplo con la función pbinom

En esta sección vamos a revisar con más detalle la función pbinom con un ejemplo completo para entender cómo calcular probabilidades binomiales en varios escenarios. Considera que un jugador de baloncesto encesta 4 de cada 10 tiros (\(p = 0.4\)). Si el jugador tira 20 veces a canasta (20 ensayos):

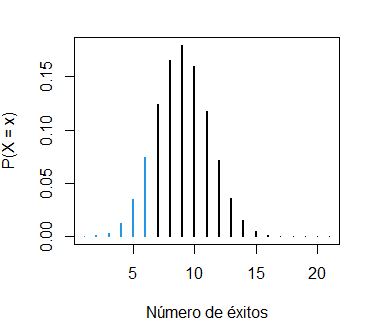
  • La probabilidad de encestar 6 canastas o menos, \(P(X \leq 6)\), es: 
pbinom(6, size = 20, prob = 0.4) # 0.2500107 o 25%
1 - pbinom(6, size = 20, prob = 0.4, lower.tail = FALSE) # Equivalente

Esta probabilidad también se puede calcular sumando los correspondientes elementos de la función de probabilidad binomial, tal y como explicamos en la sección anterior:

sum(dbinom(0:6, size = 20, prob = 0.4)) # 0.2500107 o 25%

Usando la función que definimos antes podemos representar la probabilidad calculada:

binom_sum(size = 20, prob = 0.4, ub = 6, lwd = 2,
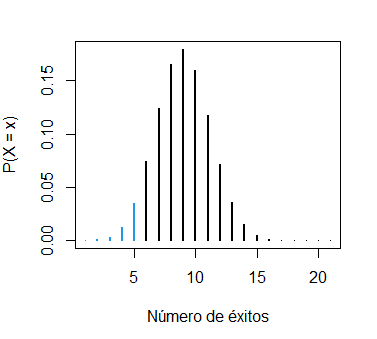
          ylab = "P(X = x)", xlab = "Número de éxitos")

Ejemplo con la función pbinom en R

  • La probabilidad de anotar menos de 6 canastas, \(P(X < 6)\), es: 
pbinom(5, size = 20, prob = 0.4) # 0.125599 o 12.56%
1 - pbinom(5, size = 20, prob = 0.4, lower.tail = FALSE) # Equivalente
sum(dbinom(0:5, size = 20, prob = 0.4)) # Equivalente

Ten en cuenta que pasamos un 5 al primer argumento de la función en lugar de un 6 porque estamos ante una distribución discreta, por lo que \(P(X < 6) = P(X \leq 5)\). La probabilidad calculada se puede representar con la suma de las siguientes probabilidades de la función de masa de probabilidad:

binom_sum(size = 20, prob = 0.4, ub = 5, lwd = 2,
          ylab = "P(X = x)", xlab = "Número de éxitos")

Función pbinom argumento lower.tail

  • La probabilidad de anotar más de 12 canastas, \(P(X > 12)\), es: 
pbinom(12, size = 20, prob = 0.4, lower.tail = FALSE) # 0.02102893 o 2.1%
1 - pbinom(12, size = 20, prob = 0.4)     # Equivalente
sum(dbinom(13:20, size = 20, prob = 0.4)) # Equivalente

Esta probabilidad corresponde a:

binom_sum(size = 20, prob = 0.4, lb = 12, lwd = 2,
          ylab = "P(X = x)", xlab = "Número de éxitos")

Suma de probabilidades binomiales en la cola derecha

  • La probabilidad de anotar entre 7 y 11 tiros, \(P(7 \leq X \leq 11)\), es: 
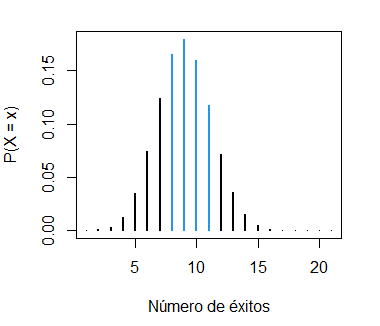
pbinom(11, size = 20, prob = 0.4) - pbinom(7, size = 20, prob = 0.4) # 0.5275807 o 52.8%
sum(dbinom(8:11, size = 20, prob = 0.4)) # Equivalente

El gráfico correspondiente se puede crear con el siguiente código:

binom_sum(size = 20, prob = 0.4, lb = 7, ub = 11, lwd = 2,
          ylab = "P(X = x)", xlab = "Número de éxitos")

Suma de probabilidades binomiales

Como la distribución binomial es una distribución discreta \(P(X = x) \neq 0\), por lo que \(P(X \geq x) \neq P(X > x)\) y \(P(X \leq x) \neq P(X < x)\).

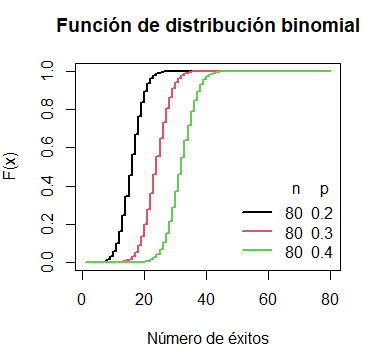
Gráfico de la función de distribución binomial acumuada en R

La función de distribución binomial se puede dibujar en R con la función plot, estableciendo type = “s” y pasando la salida de la función pbinom para un número específico de experimentos y una probabilidad de éxito.

El siguiente bloque de código se puede utilizar para dibujar el gráfico de la función de distribución acumulada para 80 ensayos de Bernoulli y diferentes probabilidades.

# Rejilla de valores del eje X
x <- 1:80

# n = 80, p = 0.2
plot(pbinom(x, size = 80, prob = 0.2), type = "s", lwd = 2,
     main = "Función de distribución binomial",
     xlab = "Número de éxitos", ylab = "F(x)")

# n = 80, p = 0.3
lines(pbinom(x, size = 80, prob = 0.3), type = "s",
      lwd = 2, col = 2)

# n = 80, p = 0.4
lines(pbinom(x, size = 80, prob = 0.4), type = "s",
      lwd = 2, col = 3)

# Añadimos una leyenda
legend("bottomright", legend = c("80  0.2", "80  0.3", "80  0.4"),
       title = "n     p", title.adj = 0.85,
       lty = 1, col = 1:3, lwd = 2, box.lty = 0)

Gráfico de la función de distribución acumulada binomial en R

La función qbinom

Dada una probabilidad o un conjunto de probabilidades, la función qbinom permite obtener el cuantil binomial correspondiente. El siguiente bloque de código describe brevemente los argumentos de la función:

qbinom(p,                 # Probabilidad o vector de probabilidades
       size,              # Número de ensayos (n > = 0)
       prob,              # Probabilidad de éxito en cada ensayo
       lower.tail = TRUE, # Si TRUE, las probabilidades son P(X <= x), o P(X > x) en otro caso
       log.p = FALSE)     # Si TRUE, las probabilidades se devuelven como log

Como ejemplo, el cuantil binomial para la probabilidad 0.4 si \(n = 5\) y \(p = 0.7\) es:

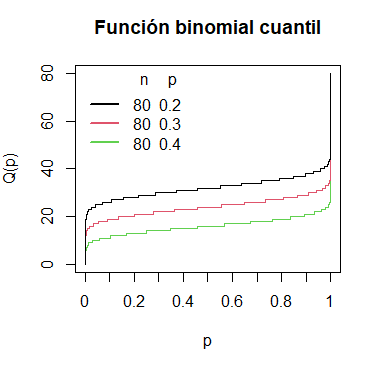
qbinom(p = 0.4, size = 5, prob = 0.7) # 3

Gráfico de la función cuantil binomial en R

La función cuantil binomial se puede dibujar en R para un conjunto de probabilidades, un número de ensayos y una probabilidad de éxito en cada ensayo con el siguiente código:

# Rejilla de valores del eje X
x <- 1:80

# size = 80, prob = 0.2
plot(qbinom(seq(0, 1, 0.001), size = 80, prob = 0.2),
     main = "Función binomial cuantil",
     ylab = "Q(p)", xlab = "p",
     type = "s", col = 3, xaxt = "n")
axis(1, labels = seq(0, 1, 0.1), at = 0:10 * 100)

# size = 80, prob = 0.3
lines(qbinom(seq(0, 1, 0.001), size = 80, prob = 0.3), type = "s", col = 2)

# size = 80, prob = 0.4
lines(qbinom(seq(0, 1, 0.001), size = 80, prob = 0.4), type = "s", col = 1)

# Añadimos una leyenda
legend("topleft", legend = c("80  0.2", "80  0.3", "80  0.4"),
       title = "n     p", title.adj = 0.85,
       lty = 1, col = 1:3, lwd = 2, box.lty = 0)

Función cuantil binomial en R

La función rbinom

Con el objetivo de obtener \(n\) observaciones aleatorias de una distribución binomial en R se puede utilizar la función rbinom. Los argumentos de la función se describen a continuación:

rbinom(n,    # Número de observaciones aleatorias a ser generadas
       size, # Número de ensayos (> = 0)
       prob) # La probabilidad de éxito en cada ensayo

Si quieres obtener, por ejemplo, 15 observaciones aleatorias de una distribución binomial si el número de ensayos es 30 y la probabilidad de éxito 0.1 puedes escribir:

rbinom(n = 15, size = 30, prob = 0.1)
7 3 2 1 5 1 1 4 4 3 1 5 2 4 1

Sin embargo, si no especificas una semilla antes de ejecutar la función obtendrás un conjunto de observaciones diferente cada vez. Si quieres que la salida sea reproducible puedes establecer la semilla como sigue:

set.seed(2)
rbinom(n = 15, size = 30, prob = 0.1)
2 4 3 1 6 6 1 5 3 3 3 2 4 1 2