Transformación de Box Cox en R
La transformación de Box-Cox es una transformación potencial que corrige la asimetría de una variable, varianzas diferentes o la no linealidad entre variables. En consecuencia, resulta muy útil para transformar una variable y obtener una nueva que siga una distribución normal.
Familia Box Cox
Las transformaciones de Box-Cox vienen dadas para diferentes valores de \(\lambda\) por la siguiente expresión:
\(\begin{cases} \frac{x^{\lambda} - 1}{\lambda} \quad \text{ si } \quad \lambda \neq 0 \\log(x) \text{ si } \quad \lambda = 0\end{cases}\),
siendo \(y\) la variable a ser transformada y \(\lambda\) el parámetro de transformación. Sin embargo, las transformaciones más habituales se describen en la siguiente tabla:
| \(\lambda\) | Transformación |
|---|---|
| -2 | \(1/x^2\) |
| -1 | \(1/x\) |
| -0.5 | \(1/\sqrt{x}\) |
| 0 | \(\log(x)\) |
| 0.5 | \(\sqrt{x}\) |
| 1 | x |
| 2 | \(x^2\) |
Si el parámetro de la transformación estimado es cercano a los valores de la tabla anterior, en la práctica es recomendable utilizar el valor de la tabla en lugar del exacto, ya que será más fácil de interpretar.
La función boxcox en R
Usando R, podemos hacer uso de la función boxcox de la librería MASS para estimar el parámetro de transformación por estimación de máxima verosimilitud. Esta función también nos mostrará el intervalo de confianza al 95% del parámetro. Los argumentos de la función son los siguientes:
boxcox(object, # Objeto lm o aov o fórmulas
lambda = seq(-2, 2, 1/10), # Vector de valores de lambda
plotit = TRUE, # Lógico. Si TRUE crea un gráfico
interp, # Lógico. Controla si se usa interpolación spline o no
eps = 1/50, # Tolerancia para lambda. Por defecto 0.02.
xlab = expression(lambda), # Título eje X
ylab = "log-Likelihood", # Título eje Y
…) # Argumentos adicionales para ajustar el modeloEjemplo de transformación Box Cox
Considera el siguiente vector de muestra x, que no sigue una distribución normal:
x <- c(0.103, 0.528, 0.221, 0.260, 0.091,
1.314, 1.732, 0.244, 1.981, 0.273,
0.461, 0.366, 1.407, 0.079, 2.266)
# Histograma de los datos
hist(x)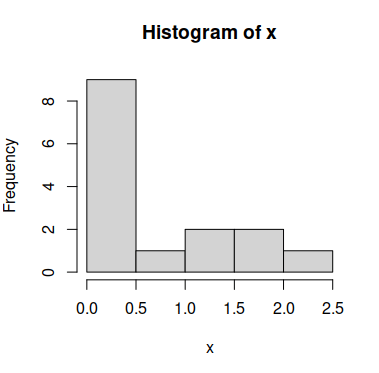
Para calcular el \(\lambda\) óptimo hay que ejecutar un modelo lineal con la función lm y pasarlo a la función boxcox de la siguiente manera:
# install.packages(MASS)
library(MASS)
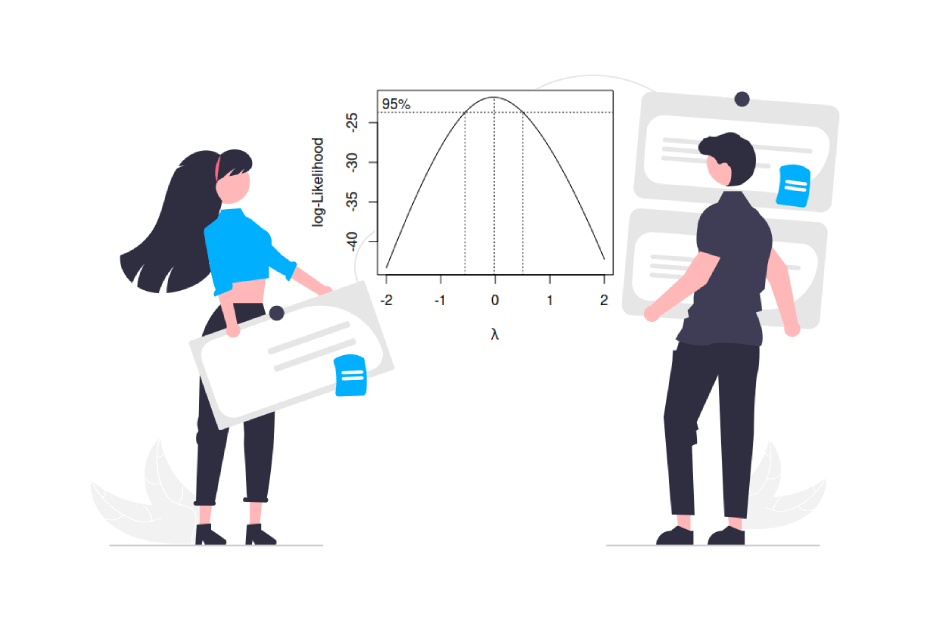
boxcox(lm(x ~ 1))La salida de la función anterior será el siguiente gráfico:
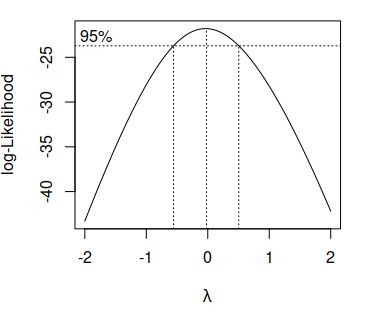
Ten en cuenta que la línea vertical punteada central representa el parámetro estimado \(\hat{\lambda}\) mientras que las otras dos representan su intervalo de confianza al 95%.
Como el gráfico anterior muestra que el 0 está dentro del intervalo de confianza del \(\lambda\) óptimo y la estimación está realmente cerca del 0, en este ejemplo la mejor opción es aplicar la transformación logarítmica a los datos (ver tabla de la primera sección).
# Datos transformados
new_x <- log(x)
# Histograma
hist(new_x)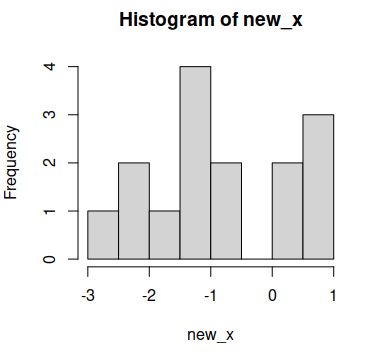
Ahora parece que los datos puedan seguir una distribución normal, pero puedes comprobarlo realizando, por ejemplo, un test estadístico como el test de Shapiro-Wilk:
shapiro.test(new.x)Shapiro-Wilk normality test
data: new_x
W = 0.9, p-value = 0.2Como el p valor es mayor que los niveles de significación usuales (1%, 5% y 10%) no existen evidencias significativas para rechazar la hipótesis nula de normalidad.
Extraer el lambda exacto
Si el intervalo de confianza no incluye ningún valor de la tabla de transformaciones habituales puedes extraer el parámetro \(\lambda\) exacto utilizando el siguiente código:
# install.packages(MASS)
library(MASS)
b <- boxcox(lm(x ~ 1))
# Lambda exacto
lambda <- b$x[which.max(b$y)] # -0.02Ahora puedes hacer la transformación de la variable haciendo uso de la expresión de la primera sección:
new_x_exact <- (x ^ lambda - 1) / lambda
new_x_exact