Tests de Wilcoxon en R con wilcox.test()

Estadística con R Contrastes de hipótesis
Test de Wilcoxon en R con wilcox.test()

La función wilcox.test en R se utiliza para realizar el test de signos (para comparar si la mediana de una muestra es igual a un valor específico y también test de muestras apareadas) y el test de Wilcoxon de sumas de rangos (también conocido como el test U de Mann-Whitney) para comparar dos muestras independientes y evaluar si sus distribuciones son estocásticamente iguales, mayores o menores entre sí.

Los contrastes de Wilcoxon son tests no paramétricos que se utilizan cuando los datos no cumplen los supuestos de los tests paramétricos, como la normalidad.

El test de Kruskal-Wallis es la generalización de la prueba de Wilcoxon para \(k\) muestras.

Sintaxis de la función wilcox.test

La función wilcox.test en R tiene la siguiente sintaxis:

wilcox.test(x, y = NULL,
            alternative = c("two.sided", "less", "greater"),
            mu = 0, paired = FALSE, exact = NULL, correct = TRUE,
            conf.int = FALSE, conf.level = 0.95,
            tol.root = 1e-4, digits.rank = Inf, ...)

Siendo:

  • x: vector numérico de datos que representan la primera muestra.
  • y: (Opcional) vector numérico de datos que representan la segunda muestra para una prueba de Mann-Whitney. Si no se especifica (NULL, por defecto), se realiza un test de Wilcoxon de una muestra sobre x.
  • alternative: hipótesis alternativa. Los posibles valores son "two.sided" (por defecto), "less" y "greater".
  • mu: la mediana hipotética (para el test de una muestra) o la diferencia de medianas entre las muestras (para el test de dos muestras).
  • paired: un valor lógico que indica si las muestras representan datos apareados.
  • exact: si se calcula un p-valor exacto. Los valores posibles son TRUE, FALSE y NULL (por defecto, que calcula un p-valor exacto para muestras de tamaño pequeño a moderado).
  • correct: un valor lógico que indica si aplicar la corrección de continuidad.
  • conf.int: un valor lógico que indica si se deben calcular intervalos de confianza.
  • conf.level: si conf.int = TRUE es el nivel de confianza del intervalo.
  • tol.root: si conf.int = TRUE es una tolerancia numérica utilizada en algunos cálculos.
  • digits.rank: número de dígitos significativos para calcular rangos.

Test de signos

El contraste de signos de Wilcoxon es una prueba estadística no paramétrica utilizada para determinar si la mediana de una muestra individual difiere significativamente de un valor hipotético (normalmente cero).

Mediana igual a un valor específico

Las hipótesis nula y alternativa en este escenario son las siguientes:

  • \(H_0\): la mediana de X ES \(\mu\).
  • \(H_1\): la mediana de X NO \(\mu\).

Siendo \(\mu\) el valor específico de la mediana a comprobar, que suele ser cero.

Considera que tienes los siguientes datos llamados x representados usando un diagrama de cajas:

# Datos de muestra
x <- c(0.22, 1.05, -0.24, 0.18, 0.16, -0.67, 2.49, -0.07, -0.13, -0.03)

# Box plot
boxplot(x, col = 4, xlab = "Muestra")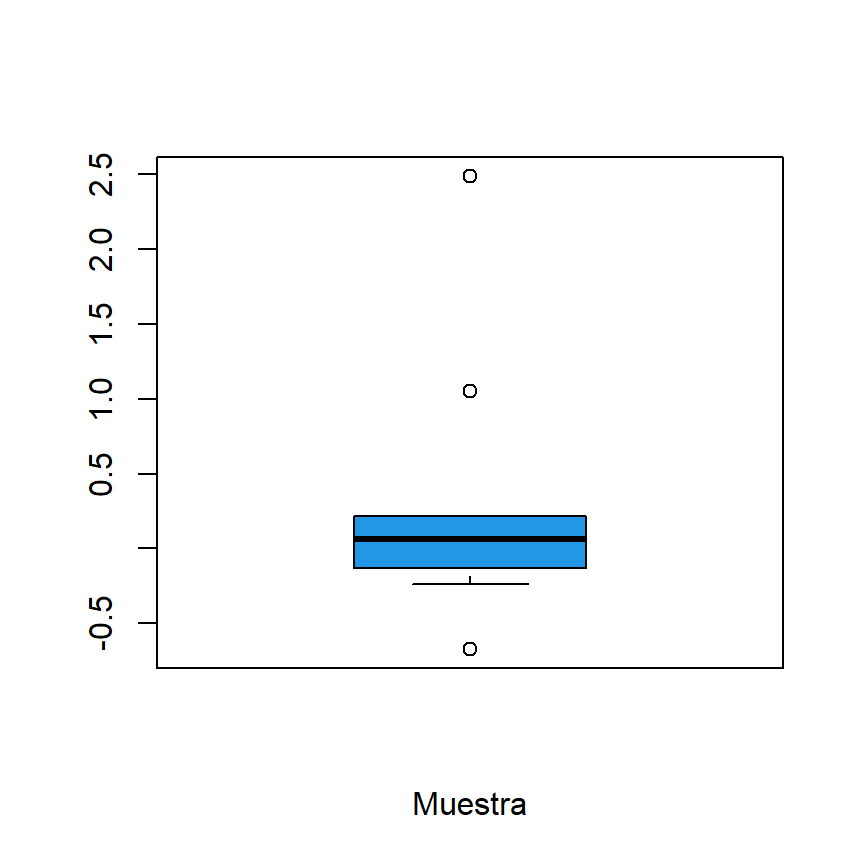

Muestra para realizar un test de signos de Wilcoxon en R

Puedes realizar un test de los rangos con signo de Wilcoxon para comprobar si la mediana de x es igual a 0:

# Datos de muestra
x <- c(0.22, 1.05, -0.24, 0.18, 0.16, -0.67, 2.49, -0.07, -0.13, -0.03)

# ¿Es la mediana de 'x' igual a 0?
wilcox.test(x, mu = 0)
	Wilcoxon signed rank exact test

data:  x
V = 34, p-value = 0.5566
alternative hypothesis: true location is not equal to 0

El test anterior devuelve un p-valor de 0.5566, superior a los niveles de significación habituales, por lo que no hay pruebas para rechazar la hipótesis nula de que la mediana de x es igual a 0.

Mediana mayor que un valor específico

El contraste anterior era un test bilateral, pero también puedes realizar tests unilaterales con el argumento alternative. Cuando alternative = "greater" las hipótesis nula y alternativa son las siguientes:

  • \(H_0\): la mediana de X es INFERIOR O IGUAL a \(\mu\).
  • \(H_1\): la mediana de X es MAYOR que \(\mu\).

El siguiente ejemplo ilustra cómo comprobar si la mediana de x es mayor que -1:

# Datos de muestra
x <- c(0.22, 1.05, -0.24, 0.18, 0.16, -0.67, 2.49, -0.07, -0.13, -0.03)

# ¿Es la mediana de 'x' mayor que -1?
wilcox.test(x, mu = -1, alternative = "greater")
	Wilcoxon signed rank exact test

data:  x
V = 55, p-value = 0.0009766
alternative hypothesis: true location is greater than -1

El p-valor es cercano a cero, lo que implica que hay pruebas estadísticas contra la hipótesis nula de que la mediana de X es menor o igual que -1.

Mediana menor que un valor específico

La última opción es establecer alternative = "less". En este escenario las hipótesis nula y alternativa son:

  • \(H_0\): la mediana de X es MAYOR O IGUAL que \(\mu\).
  • \(H_1\): la mediana de X es MENOR que \(\mu\).

El siguiente código realiza una prueba de Wilcoxon para comprobar si la mediana de x es menor que 0:

# Datos de muestra
x <- c(0.22, 1.05, -0.24, 0.18, 0.16, -0.67, 2.49, -0.07, -0.13, -0.03)

# ¿Es la mediana de 'x' menor que 0?
wilcox.test(x, mu = 0, alternative = "less")
	Wilcoxon signed rank exact test

data:  x
V = 34, p-value = 0.7539
alternative hypothesis: true location is less than 0

La función devuelve un p-valor de 0.7539, superior a los niveles de significación habituales. Por lo tanto, no hay pruebas para rechazar la hipótesis nula de que la mediana de x es mayor o igual que 0.

Muestras apareadas

El test de signos de Wilcoxon también puede calcularse para dos grupos relacionados u observaciones apareadas (X e Y) para determinar si sus medianas son significativamente diferentes. Para realizar esta prueba tendrás que introducir dos vectores de datos y establecer paired = TRUE. Las hipótesis son las siguientes:

  • \(H_0\): la mediana de X ES IGUAL a la mediana de Y (la diferencia de medianas es 0).
  • \(H_1\): la mediana de X ES DIFERENTE de la mediana de Y (la diferencia de medianas es distinta de 0).
# Datos de muestra
x <- c(0.22, 1.05, -0.24, 0.18, 0.16, -0.67, 2.49, -0.07, -0.13, -0.03)
y <- c(0.98, -1.25, 0.03, 0.25, -0.72, 1.33, 0.81, 0.09, -0.04, -1.31)

# ¿Es la mediana de 'x' igual a la mediana de 'y'? (Muestras apareadas)
wilcox.test(x, y, mu = 0, paired = TRUE)
	Wilcoxon signed rank exact test

data:  x and y
V = 31, p-value = 0.7695
alternative hypothesis: true location shift is not equal to 0

La prueba arroja un p-valor de 0.7695, lo que implica que no hay pruebas estadísticas para rechazar la hipótesis nula de que las medianas son iguales (la diferencia de medianas es cero).

Test de sumas de rangos de Wilcoxon (test U de Mann-Whitney) para dos muestras

El contraste de suma de rangos de Wilcoxon, también conocido como prueba U de Mann-Whitney, compara las distribuciones de dos muestras independientes. Se utiliza cuando no se cumplen los supuestos del t-test (como la normalidad y la igualdad de varianzas).

Medianas iguales (distribuciones iguales)

Las hipótesis nula y alternativa en este escenario son las siguientes:

  • \(H_0\): la mediana de X ES IGUAL a la mediana de Y.
  • \(H_1\): la mediana de X ES DIFERENTE a la mediana de Y.

Observa que las hipótesis anteriores pueden reformularse utilizando lo que se conoce como location shift de \(\mu\) (normalmente \(\mu = 0\), lo que implica medianas iguales):

  • \(H_0\): el location shift entre X e Y ES \(\mu\).
  • \(H_1\): el location shift entre X e Y NO ES \(\mu\).

Para los siguientes ejemplos vamos a utilizar dos muestras independientes denominadas x e y representadas en el diagrama de cajas de abajo.

# Datos de muestra
x <- c(0.22, 0.8, -0.24, 0.18, 0.16, -0.67, 1.19, -0.07, -0.13, -0.03)
y <- c(0.19, 3.00, 1.34, 1.35, 1.95, 1.63, 0.68, 0.51, 1.65, 0.92)

# Box plot
boxplot(x, y, col = 4, names = c("Muestra 1","Muestra 2"))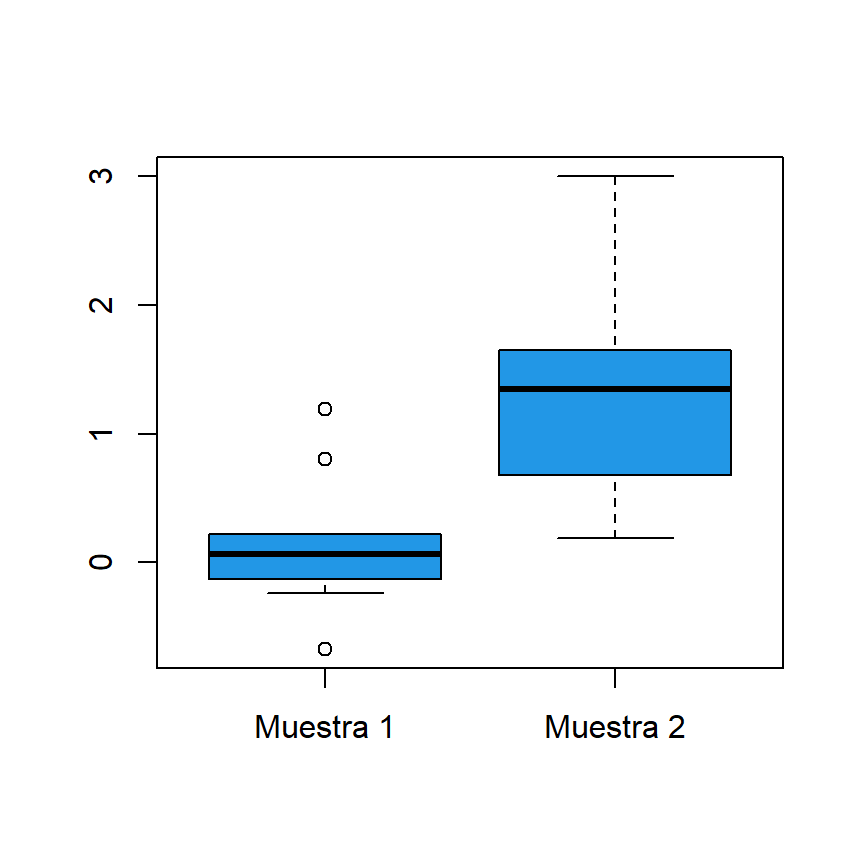

Muestras para realizar un contraste de Wilcoxon de sumas de rangos (prueba U de Mann-Whitney) en R

Para contrastar si las dos muestras tienen la misma distribución (medianas iguales) puedes introducir ambos vectores en la función wilcox.test, como se muestra a continuación.

# Datos de muestra
x <- c(0.22, 0.8, -0.24, 0.18, 0.16, -0.67, 1.19, -0.07, -0.13, -0.03)
y <- c(0.19, 3.00, 1.34, 1.35, 1.95, 1.63, 0.68, 0.51, 1.65, 0.92)

# ¿Es la mediana de 'x' igual a la mediana de 'y'?
wilcox.test(x, y)
	Wilcoxon rank sum exact test

data:  x and y
W = 8, p-value = 0.0007253
alternative hypothesis: true location shift is not equal to 0

El p-valor es inferior a los niveles de significación habituales, por lo que hay pruebas en contra de la hipótesis nula de que la mediana de x es igual a la mediana de y. Esto sugiere que es probable que las medianas de las dos muestras no sean iguales, lo que indica una diferencia en las tendencias centrales entre los grupos.

Mediana de X mayor que la mediana de Y

Para el caso unilateral, cuando alternative = "greater" las hipótesis son las siguientes:

  • \(H_0\): la mediana de X ES MENOR O IGUAL que la mediana de Y.
  • \(H_1\): la mediana de X ES MAYOR que la mediana de Y.

El siguiente bloque de código muestra cómo realizar un test de sumas de rangos de Wilcoxon para comprobar si la mediana de x es mayor que la mediana de y.

# Datos de muestra
x <- c(0.22, 0.8, -0.24, 0.18, 0.16, -0.67, 1.19, -0.07, -0.13, -0.03)
y <- c(0.19, 3.00, 1.34, 1.35, 1.95, 1.63, 0.68, 0.51, 1.65, 0.92)

# ¿Es la mediana de 'x' mayor que la mediana de 'y'?
wilcox.test(x, y, alternative = "greater")
	Wilcoxon rank sum exact test

data:  x and y
W = 8, p-value = 0.9998
alternative hypothesis: true location shift is greater than 0

Mediana de X menor que la mediana de Y

La última opción es establecer alternative = "less", que tiene las siguientes hipótesis:

  • \(H_0\): la mediana de X ES MAYOR O IGUAL que la mediana de Y.
  • \(H_1\): la mediana de X ES MENOR que la mediana de Y.

Escribe lo siguiente para comprobar si la mediana de x es menor que la mediana de y (la diferencia es menor que 0):

# Datos de muestra
x <- c(0.22, 0.8, -0.24, 0.18, 0.16, -0.67, 1.19, -0.07, -0.13, -0.03)
y <- c(0.19, 3.00, 1.34, 1.35, 1.95, 1.63, 0.68, 0.51, 1.65, 0.92)

# ¿Es la mediana de 'x' menor que la mediana de 'y'?
wilcox.test(x, y, alternative = "less")
	Wilcoxon rank sum exact test

data:  x and y
W = 8, p-value = 0.0003626
alternative hypothesis: true location shift is less than 0

El p-valor es cercano a cero, lo que implica que hay pruebas para rechazar la hipótesis nula de que la mediana de x es mayor o igual que la mediana de y. Por lo tanto, tenemos pruebas estadísticas suficientes a favor de la hipótesis alternativa, lo que indica una probable diferencia en las medianas de las dos muestras, siendo probable que x tenga una mediana menor que y.