Test de Kruskal Wallis (H test) en R

La función kruskal.test se utiliza para realizar la prueba de Kruskal-Wallis en R, también conocida como prueba H o ANOVA unidireccional. Esta prueba no paramétrica evalúa si existen diferencias estadísticamente significativas entre dos o más grupos independientes con respecto a sus medianas utilizando rangos. Es la generalización de la prueba de Wilcoxon (también conocida como prueba U de Mann-Whitney) para \(k\) muestras independientes.
La prueba de Kruskal-Wallis se recomienda cuando los datos no cumplen los requisitos para realizar un test ANOVA.
Supuestos de la prueba H de Kruskal-Wallis
El test de Kruskal-Wallis parte de los siguientes supuestos:
- Independencia: las observaciones dentro de los grupos y entre ellos son independientes.
- Datos ordinales o continuos: la variable objeto de estudio debe medirse en una escala ordinal o continua.
- Homogeneidad de varianzas: la varianza de la variable dependiente debe ser aproximadamente igual en todos los grupos.
- Muestreo aleatorio: los datos deben obtenerse a partir de una muestra aleatoria de la población.
- No se requiere normalidad.
Comprueba la homogeneidad de las varianzas con el test de Bartlett (bartlett.test()) si las muestras proceden de distribuciones normales o con el test de Levene (leveneTest() del paquete car) en caso contrario.
Hipótesis
El test de Kruskal-Wallis evalúa si existen diferencias en las distribuciones entre los grupos en función de los parámetros de localización. En esencia, la hipótesis nula supone medianas iguales entre los grupos, mientras que la hipótesis alternativa sugiere desigualdad entre las medianas. Esto es:
- \(H_0\): las medianas de todos los grupos son iguales.
- \(H_1\): al menos la mediana de un grupo es diferente de las demás.
Sintaxis de la función kruskal.test
La sintaxis de la función kruskal.test es la siguiente:
kruskal.test(x, g, ...)
# Con una fórmula:
kruskal.test(formula, data, subset, na.action, ...)Siendo:
x: vector numérico o lista lista de vectores numéricos donde cada elemento son los datos de un grupo diferente.g: vector de caracteres o factor que contiene los grupos para los elementos correspondientes dex. Se ignora sixes una lista.formula: una fórmula. La variable respuesta se encuentra en el lado izquierdo y la variable que define los grupos en el lado derecho.data: un data frame opcional que contiene las variables utilizadas en la fórmula. Si no se proporciona, las variables deben estar presentes en el entorno.subset: un vector opcional que especifica un subconjunto de observaciones.na.action: función para tratar los valores faltantes....: argumentos adicionales.
Ejemplo práctico
Para este ejemplo vamos a utilizar el conjunto de datos chickwts, que proporciona 71 observaciones de pesos de pollos (weight) por tipo de pienso (feed, 6 grupos).
El primer paso antes de realizar el contraste de Kruskal-Wallis es hacer un análisis exploratorio previo de los datos:
# Datos de muestra
df <- chickwts
# Box plot
boxplot(df$weight ~ df$feed, col = 4, xlab = "Group", ylab = "Value")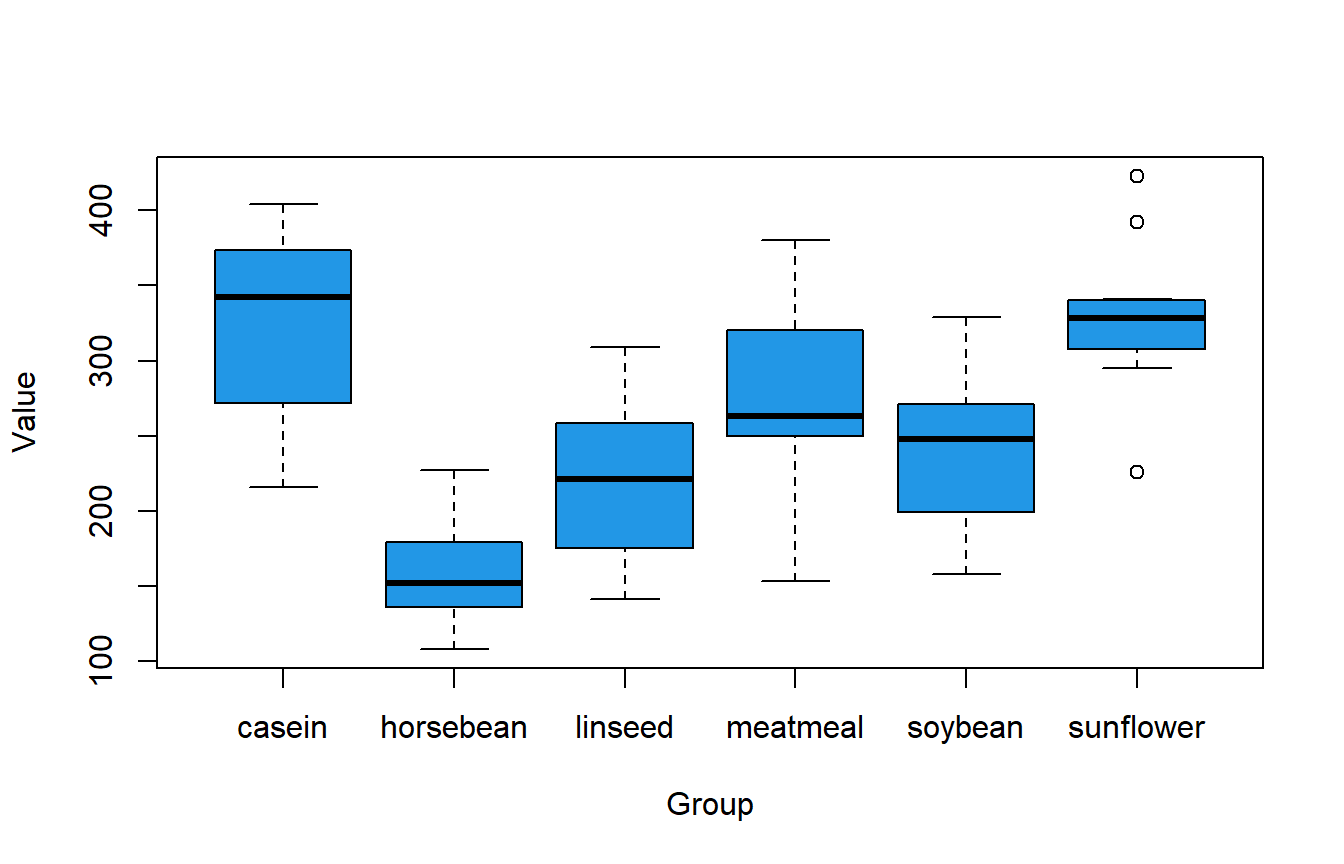
El box plot anterior ilustra las diferencias potenciales entre grupos. Además, la función tapply permite crear resúmenes estadísticos muestrales, como los valores mínimo y máximo, la media y los cuartiles por grupo.
# Datos de muestra
df <- chickwts
tapply(df$weight, df$feed, summary)$casein
Min. 1st Qu. Median Mean 3rd Qu. Max.
216.0 277.2 342.0 323.6 370.8 404.0
$horsebean
Min. 1st Qu. Median Mean 3rd Qu. Max.
108.0 137.0 151.5 160.2 176.2 227.0
$linseed
Min. 1st Qu. Median Mean 3rd Qu. Max.
141.0 178.0 221.0 218.8 257.8 309.0
$meatmeal
Min. 1st Qu. Median Mean 3rd Qu. Max.
153.0 249.5 263.0 276.9 320.0 380.0
$soybean
Min. 1st Qu. Median Mean 3rd Qu. Max.
158.0 206.8 248.0 246.4 270.0 329.0
$sunflower
Min. 1st Qu. Median Mean 3rd Qu. Max.
226.0 312.8 328.0 328.9 340.2 423.0 Ahora tendrás que contrastar la igualdad de varianzas entre los grupos. Para ello, puedes utilizar la prueba de Bartlett (se requiere normalidad) o la de Levene, que es más robusta:
# Datos de muestra
df <- chickwts
library(car)
leveneTest(df$weight ~ df$feed)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 0.7493 0.5896
65 La test devuelve un p-valor superior a los niveles de significación habituales, por lo que no hay pruebas estadísticas para rechazar la hipótesis nula de homogeneidad de varianzas.
Una vez que sepas que los datos cumplen los supuestos puedes realizar el test de Kruskal-Wallis con la función kruskal.test de la siguiente manera:
# Datos de muestra
df <- chickwts
# ¿Es la mediana de 'weight' igual entre todos los grupos de 'feed'?
kruskal.test(df$weight ~ df$feed)
# Equivalente a:
# kruskal.test(weight ~ feed, data = df)
# kruskal.test(x = df$weight, g = df$feed)
# kruskal.test(x = split(df$weight, df$feed, drop = TRUE)) # Lista Kruskal-Wallis rank sum test
data: df$weight by df$feed
Kruskal-Wallis chi-squared = 37.343, df = 5, p-value = 5.113e-07El p-valor es próximo a cero, lo que implica la existencia de pruebas sólidas contra la hipótesis nula de igualdad de medianas entre los grupos.
El test de Kruskal-Wallis no indica qué grupo específico difiere; sólo determina si existe una diferencia significativa entre los grupos. Es posible que se necesiten más pruebas post-hoc o comparaciones por pares para identificar diferencias específicas entre grupos después de rechazar la hipótesis nula.
Comparaciones post-hoc
El resultado de la prueba de Kruskal-Wallis indica que las medianas de los grupos no son iguales. Sin embargo, esta prueba no especifica qué grupos difieren. Para identificar los grupos que difieren, puedes utilizar la función pairwise.wilcox.test, que realiza pruebas de Wilcoxon para cada par de grupos.
pairwise.wilcox.test(x = df$weight, g = df$feed) Pairwise comparisons using Wilcoxon rank sum exact test
data: df$weight and df$feed
casein horsebean linseed meatmeal soybean
horsebean 0.00030 - - - -
linseed 0.01221 0.05001 - - -
meatmeal 0.36337 0.00306 0.21806 - -
soybean 0.04736 0.00834 0.70996 0.70996 -
sunflower 1.00000 9.3e-05 0.00064 0.34409 0.01402
P value adjustment method: holm La función devolverá una matriz de p-valores. Si el p-valor correspondiente es inferior a los niveles de significación habituales, existe una fuerte evidencia en contra de la igualdad de medianas para ese par de grupos. Por ejemplo, el primer p-valor (0.00030) indica que los grupos denominados horsebean y casein no tienen la misma mediana.