Test chi-cuadrado de Pearson en R con chisq.test()
La función chisq.test de R realiza contrastes chi-cuadrado de Pearson para la independencia, la bondad de ajuste y la homogeneidad, analizando relaciones entre datos categóricos. La función también admite la corrección de Yates y la simulación Monte Carlo para los p-valores.
Sintaxis
La función chisq.test para realizar tests chi-cuadrado de Pearson en R tiene la siguiente sintaxis:
chisq.test(x, y = NULL, correct = TRUE,
p = rep(1/length(x), length(x)), rescale.p = FALSE,
simulate.p.value = FALSE, B = 2000)Siendo:
x: una tabla de contingencia, data frame, matriz o vector.y: opcionalmente, una segunda variable para realizar una prueba de independencia en una tabla de contingencia.correct: lógico. Si esTRUE(por defecto), aplica la corrección de continuidad de Yates para tablas de contingencia 2x2.p: vector de probabilidades para una prueba de bondad de ajuste.rescale.p: lógico. Si esTRUE, reescala las probabilidades para que sumen 1.simulate.p.value: lógico. Si esTRUE, calcula el p-valor utilizando la simulación Monte Carlo.B: número de réplicas para la simulación Monte Carlo.
Test chi-cuadrado de independencia
Este contraste de hipótesis se utiliza para determinar si existe una asociación significativa entre dos variables categóricas. Evalúa si la distribución de frecuencias de una variable depende de la distribución de otra variable. Las hipótesis nula y alternativa son las siguientes:
- \(H_0\): las variables categóricas SON INDEPENDIENTES en la población.
- \(H_1\): las variables categóricas SON DEPENDIENTES en la población.
Considera que tienes 100 productos clasificados por calidad y precio alto-bajo:
| Precio\calidad | Calidad alta | Calidad baja |
|---|---|---|
| Precio alto | 40 | 10 |
| Precio bajo | 20 | 30 |
La tabla anterior se puede crear y representar en R con el siguiente código:
# Datos de ejemplo
datos <- matrix(c(40, 20, 10, 30), nrow = 2)
rownames(datos) <- c("Precio alto", "Precio bajo")
colnames(datos) <- c("Calidad alta", "Calidad baja")
# Gráfico de barras
barplot(datos, col = 3:4, beside = TRUE, ylab = "Frecuencia")
legend("topright", rownames(datos), fill = 3:4)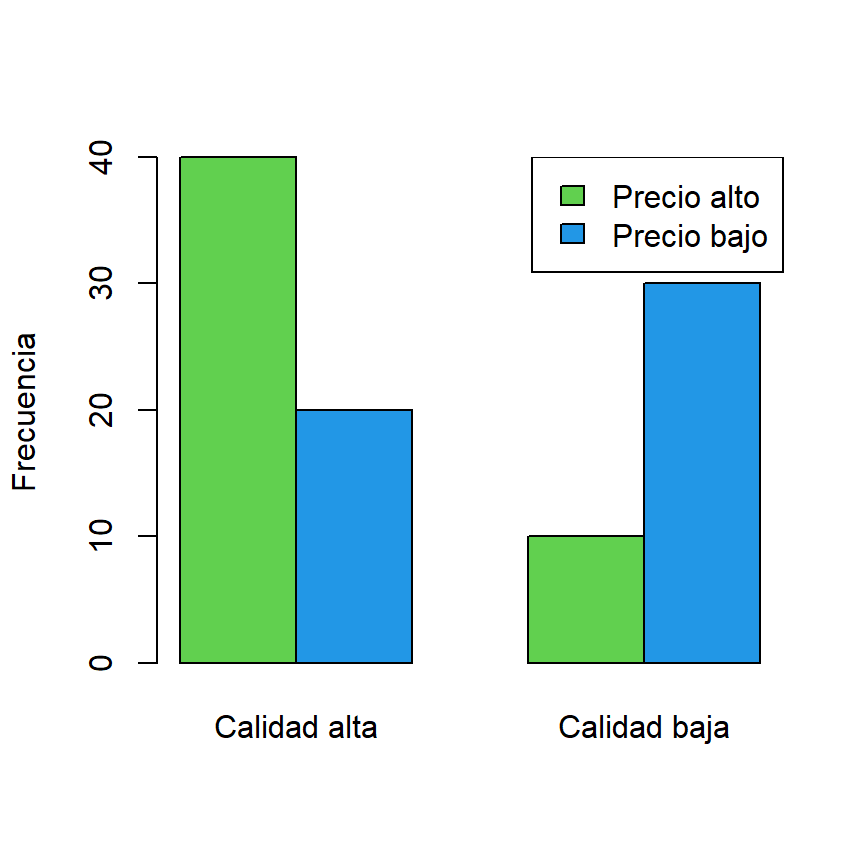
Ahora, si quieres comprobar si la calidad y los precios son independientes puedes realizar un test chi-cuadrado pasando la tabla o matriz con los datos a la función chisq.test.
# Datos de ejemplo
datos <- matrix(c(40, 20, 10, 30), nrow = 2)
rownames(datos) <- c("Precio alto", "Precio bajo")
colnames(datos) <- c("Calidad alta", "Calidad baja")
# Contraste chi-cuadrado para la independencia
chi <- chisq.test(datos)
chi Pearson's Chi-squared test with Yates' continuity correction
data: datos
X-squared = 15.042, df = 1, p-value = 0.0001052El p-valor es casi cero, por lo que hay pruebas significativas para rechazar la hipótesis nula de que no existe asociación entre las variables sometidas a prueba. Por lo tanto, es probable que exista una asociación entre calidad y precio.
Ten en cuenta que también puedes devolver los recuentos esperados y los residuos de Pearson:
# Frecuencias esperadas bajo H0
chi$expected
# Calidad alta Calidad baja
# Precio alto 30 20
# Precio bajo 30 20
# Residuos de Pearson
chi$residuals
# Calidad alta Calidad baja
# Precio alto 1.825742 -2.236068
# Precio bajo -1.825742 2.236068
# Residuos estandarizados
chi$stdres
# Calidad alta Calidad baja
# Precio alto 4.082483 -4.082483
# Precio bajo -4.082483 4.082483Quizás hayas observado que la prueba anterior se realizó con la corrección de continuidad de Yates. Establece correct = FALSE para evitar aplicar esta corrección.
Se recomienda utilizar la prueba exacta de Fisher (fisher.test()) para tablas de contingencia 2x2 en lugar del test Chi-cuadrado cuando el tamaño de la muestra es pequeño (\(n < 30\)) o cuando las frecuencias esperadas son inferiores a 5.
Test chi-cuadrado para la bondad de ajuste
Esta prueba examina si una distribución de frecuencias observada coincide con una distribución teórica esperada, como la distribución uniforme o cualquier otra distribución. Este test extiende el contraste para una proporción.
Las hipótesis son las siguientes
- \(H_0\): la distribución de la población ES F.
- \(H_1\): la distribución de la población NO ES F.
Si tienes un vector con frecuencias observadas, puedes realizar un test chi-cuadrado para comprobar si las frecuencias observadas se ajustan a las probabilidades esperadas (teóricas):
observadas <- c(11, 32, 24) # Frecuencias observadas
esperadas <- c(0.2, 0.5, 0.3) # Probabilidades esperadas (suman 1)
# Test chi-cuadrado para la bondad de ajuste (¿Son las probabilidades poblacionales iguales a 'p'?)
chisq.test(x = observadas, p = esperadas) Chi-squared test for given probabilities
data: observadas
X-squared = 1.2537, df = 2, p-value = 0.5343El p-valor es superior a los niveles de significación habituales, por lo que no hay pruebas para rechazar la hipótesis nula.
Ten en cuenta que también puedes introducir frecuencias esperadas en lugar de probabilidades si estableces rescale.p = TRUE, ya que las frecuencias se reescalarán si es necesario para que sumen 1.
observadas <- c(11, 32, 24) # Frecuencias observadas
esperadas <- c(20, 53, 25) # Frecuencias esperadas
# Chi-squared test for goodness of fit with rescaled 'p'
chisq.test(x = observadas, p = esperadas, rescale.p = TRUE)Por último, si no se especifica p, se contrastará si todas las probabilidades son iguales (distribución uniforme).
observadas <- c(15, 25, 20)
# ¿Son las probabilidades poblacionales iguales? (¿Es la población uniforme?)
chisq.test(observadas) Chi-squared test for given probabilities
data: observadas
X-squared = 2.5, df = 2, p-value = 0.2865El test devuelve un p-valor de 0.2865, superior a los niveles de significación habituales. Por lo tanto, no hay pruebas estadísticas para rechazar la hipótesis nula de igualdad de probabilidades.
Test chi-cuadrado de homogeneidad
Este contraste compara las distribuciones de una única variable categórica entre varios grupos o poblaciones independientes. Determina si la distribución de frecuencias de una única variable categórica es similar u homogénea entre diferentes grupos. Esta prueba expande el test para dos proporciones.
Las hipótesis son las siguientes:
- \(H_0\): las distribuciones de dos o más subgrupos de una población SON iguales (proporciones iguales).
- \(H_1\): las distribuciones de dos o más subgrupos de una población SON DIFERENTES (al menos una proporción es diferente).
El test chi-cuadrado de independencia y el test chi-cuadrado de homogeneidad son matemáticamente iguales, pero difieren en una cuestión de diseño. Mientras que la prueba de independencia examina la relación entre dos variables categóricas en una única población, el contraste de homogeneidad evalúa si la distribución de una variable categórica es homogénea o consistente entre diferentes poblaciones o grupos.
Considera que quieres comprobar si la distribución de frecuencias de un tratamiento es igual o diferente entre grupos de edad (es decir, si la proporción de uso de varios fármacos es igual o diferente entre grupos de edad). Se tienen los siguientes datos de uso de fármacos en dos grupos de edad:
| Fármaco A | Fármaco B | Fármaco C | |
|---|---|---|---|
| Menos de 30 años | 18 | 26 | 44 |
| Más de 30 años | 6 | 14 | 19 |
Los datos anteriores se pueden crear y representar en R con el siguiente código:
# Datos de ejemplo
datos <- matrix(c(18, 26, 44, 6, 14, 19), nrow = 2, byrow = TRUE)
colnames(datos) <- c("Fármaco A", "Fármaco B", "Fármaco C")
rownames(datos) <- c("Menos de 30 años", "Más de 30 años")
# Gráfico de barras
barplot(datos, beside = TRUE, col = 2:3,
xlab = "Tratamiento", ylab = "Frecuencia")
legend("topleft", rownames(datos), fill = 2:3)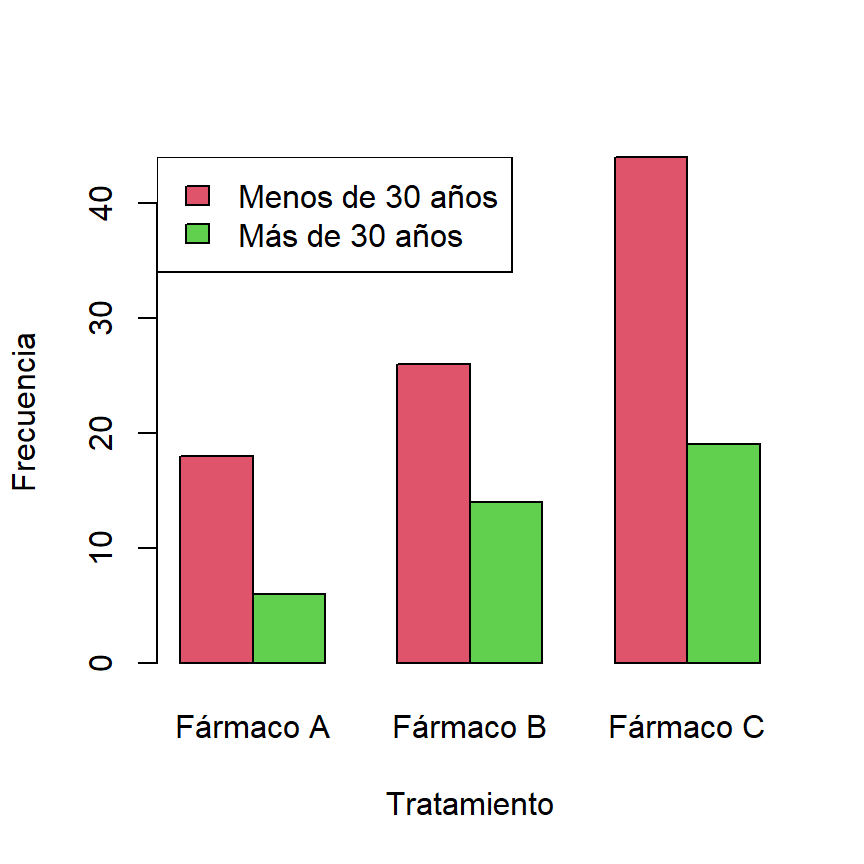
Ahora, puedes realizar una prueba de chi-cuadrado como se ilustra a continuación:
# Datos de ejemplo
datos <- matrix(c(18, 26, 44, 6, 14, 19), nrow = 2, byrow = TRUE)
colnames(datos) <- c("Fármaco A", "Fármaco B", "Fármaco C")
rownames(datos) <- c("Menos de 30 años", "Más de 30 años")
# Test chi-cuadrado de homogeneidad
chisq.test(datos) Pearson's Chi-squared test
data: datos
X-squared = 0.72271, df = 2, p-value = 0.6967El p-valor es 0.6967, superior a los niveles de significación habituales, por lo que no hay pruebas para rechazar la hipótesis nula de que la distribución es igual entre los grupos de edad.
Cuando sea necesario, recuerda establecer simulate.p.value = TRUE para calcular los p-valores mediante simulación Monte Carlo con B réplicas (por defecto B = 2000).