Rango intercuartílico en R

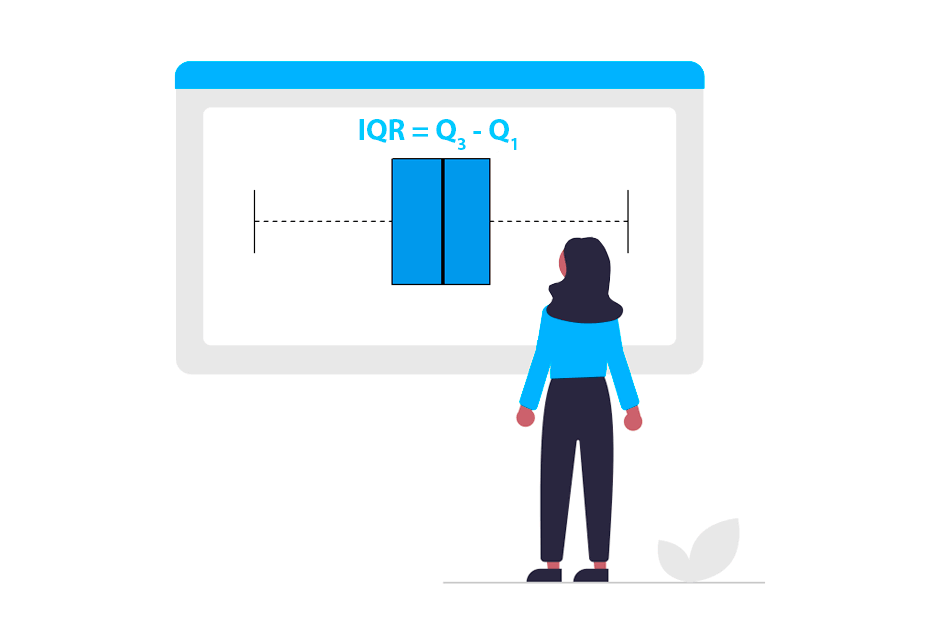
El rango intercuartílico es una medida de dispersión estadística, concretamente la diferencia entre el tercer cuartil (\(Q_3\)) y el primer cuartil (\(Q_1\)): \[IQR = Q_3 - Q_1\] Esta medida puede calcularse en R con la función IQR.

Sintaxis

El rango intercuartílico puede calcularse en R con la función IQR, que tiene la siguiente sintaxis:

IQR(x,             # Vector numérico
    na.rm = FALSE, # Si TRUE, se eliminan los valores faltantes
    type = 7)      # Número entero entre 1 y 9 que selecciona un algoritmo cuantílico

En la siguiente sección vamos a ilustrar el uso de esta función con algunos ejemplos.

Ejemplos

Rango intercuartílico de un vector

Dado un vector x puedes introducirlo en la función IQR para calcular su rango intercuartílico:

# Datos de muestra
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Rango intercuartílico de 'x'
IQR(x)

16

La función devuelve 16. Vamos a calcularlo manualmente utilizando la función quantile para entenderlo mejor:

# Datos de muestra
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Cuartiles de 'x'
Q <- quantile(x)
Q

  0%  25%  50%  75% 100% 
 1.0  3.5 16.5 19.5 24.0 

El rango intercuartílico se calcula como el tercer cuartil (19.5) menos el primer cuartil (3.5), es decir:

# Rango intercuartílico de 'x'
Q[4] - Q[2]

# Equivalente a:
# quantile(x, probs = 0.75) - quantile(x, probs = 0.25)

75% 
 16 

Ten en cuenta que también puedes especificar otro algoritmo para calcular cuantiles haciendo uso de type, que toma un entero de 1 a 9 como entrada. El siguiente ejemplo calcula el rango intercuartílico de x con el algoritmo tipo 8.

# Datos de muestra
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Rango intercuartílico de 'x' con el algoritmo tipo 8
IQR(x, type = 8)

17.33333

Rango intercuartílico con datos faltantes

Si tus datos contienen valores omitidos, puedes establecer na.rm = TRUE para eliminarlos del cálculo.

# Datos de muestra
x <- c(19, 21, NA, 1, 4, 2, NA, 24)

# Rango intercuartílico de 'x' con valores omitidos
IQR(x, na.rm = TRUE)

18

Rango intercuartílico de las columnas de un data frame

Es posible calcular el rango intercuartílico de las columnas de un data frame utilizando la función apply por columnas de la siguiente manera:

# Datos de muestra
df <- data.frame(x = rnorm(10), y = rexp(10), z = runif(10))

# Rango intercuartílico de las columnas de un data frame
apply(df, 2, IQR)

        x         y         z 
2.6869600 0.6245126 0.3334760 

Rango semi-intercuartílico

El rango semi-intercuartílico (SIQR por sus siglas en inglés) es el rango intercuartílico dividido por dos. Esto es:

\[SIQR = \frac{(Q_3 - Q_1)}{2}\]

Para más información, revisa el ejemplo siguiente:

# Datos de muestra
x <- c(19, 21, 16, 1, 4, 2, 17, 24)

# Rango semi-intercuartílico de 'x'
SIQR <- IQR(x) / 2
SIQR

8