Estimar la moda en R

La moda es una medida de localización que se define como el valor más probable de una variable aleatoria o como el valor más frecuente de un conjunto de observaciones. Es una medida robusta que coincide con la media y con la mediana en distribuciones simétricas. En este tutorial revisaremos como calcular la moda en R tanto para variables unidimensionales tanto discretas como continuas.

Estimación unimodal discreta

Considera que tienes el siguiente vector x:

x <- c(1, 5, 1, 6, 2, 1, 6, 7, 1)

La moda se calcula como el valor más repetido dentro de la variable, que en este caso es 1. Una manera sencilla de calcular la moda en R es usar la siguiente función:

mode <- function(x) {
   return(as.numeric(names(which.max(table(x)))))
}

En este caso, podemos comprobar que la moda es 1 pasando el vector a la función:

mode(x) # 1

Si queremos visualizar el número de veces que se repite cada dato también podemos crear un gráfico de barras:

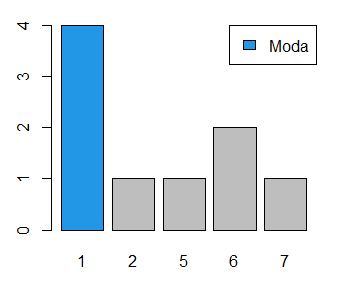
barplot(table(x), col = c(4, rep("gray", 4)))
legend("topright", "Moda", fill = 4)

Estimación unimodal continua

Si nuestra variable de interés es continua en lugar de discreta no podremos utilizar el procedimiento anterior, sino que debemos recurrir a otro método. El procedimiento más habitual en la literatura es calcular el máximo de la estimación de la función de densidad de los datos mediante algún algoritmo.

Consideremos los siguientes datos normales (unimodales) con media 0 y desviación típica 1. Como la distribución normal es simétrica, sabemos que la media, la mediana y la moda son iguales (0).

set.seed(1234)
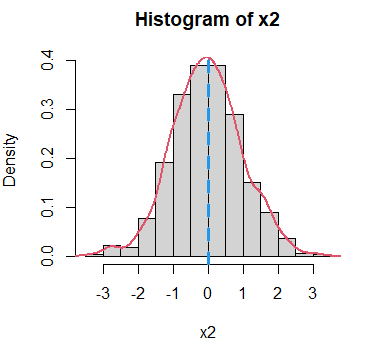
x2 <- rnorm(1000)

Para visualizar las modas podemos dibujar el histograma y la estimación de la función de densidad de los datos. Ten en cuenta que la selección del parámetro ventana determinará la forma de la densidad estimada.

# Histograma
hist(x2, freq = FALSE)
# Densidad
dx <- density(x2)
lines(dx$x, dx$y, col = 2, lwd = 2)
# Moda teórica
abline(v = 0, col = 4, lty = 2, lwd = 3)

Para realizar el cálculo recomendamos recurrir a la función mlv de la librería modeest, que nos permite seleccionar entre diferentes algoritmos. Nosotros aconsejamos utilizar el algoritmo mean-shift como se indica en el siguiente bloque.

# install.packages("modeest")
library(modeest)

# Moda
mlv(x2, method = "meanshift") # -0.03912067

Podemos observar que la moda estimada (-0.039) es muy próxima a la moda teórica (0). Otros métodos disponibles son “lientz”, “naive”, “venter”, “grenander”, “hsm”, “parzen”, “tsybakov” y “asselin”.

Estimación multimodal discreta

A diferencia de la mediana o la media, la moda puede tomar varios valores a la vez. Como ejemplo, considera el vector y, donde hay dos modas.

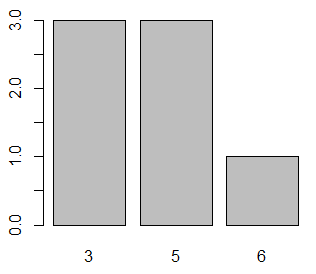
y <- c(3, 5, 3, 3, 5, 6, 5)

# Histograma
hist(y)

En este caso los valores más repetidos son 3 y 5. Para calcular varias modas podemos recurrir a la función mlv del paquete modeest y aplicar el método mfv.

# install.packages("modeest")
library(modeest)

# Modas
mlv(y, method = "mfv") # 3 5 

Estimación multimodal continua

Si queremos calcular varias modas en el caso de tener una variable continua podemos recurrir a la función locmodes de la librería multimode.

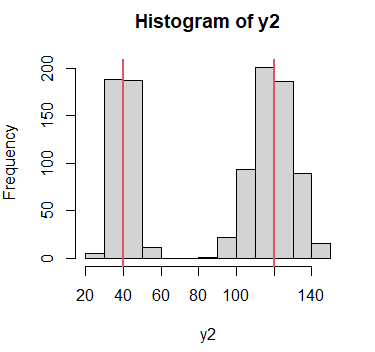
Considera los siguientes datos multimodales, cuyas modas teóricas son 40 y 120, representadas con líneas rojas verticales.

n <- 1000
bin <- rbinom(n, 1, 0.6)
y2 <- rnorm(n, mean = 120, sd = 11) * bin +
      rnorm(n, mean = 40, sd = 5) * (1 - bin)

# Histograma
hist(y2)
# Moda teórica 1
abline(v = 40, col = 2, lwd = 2) 
# Moda teórica 2
abline(v = 120, col = 2, lwd = 2)

A los datos anteriores les podemos aplicar la función locmodes, indicando el número de modas que esperamos encontrar en el argumento mod0.

# install.packages("multimode")
library(multimode)

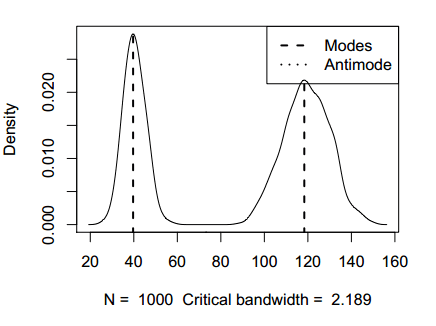
modas <- locmodes(y2, mod0 = 2)
modas

Estimated location
Modes: 40.56825  120.8625 
Antimode: 69.94661 

Estimated value of the density
Modes: 0.02535653  0.02033563 
Antimode: 8.184294e-08 

Critical bandwidth: 3.746696

Warning message:
In locmodes(y, mod0 = 2) :
  If the density function has an unbounded support, artificial modes may have been created in the tails

En la salida anterior podemos observar que las modas estimadas son 40.57 y 120.86, muy próximas a los valores teóricos.

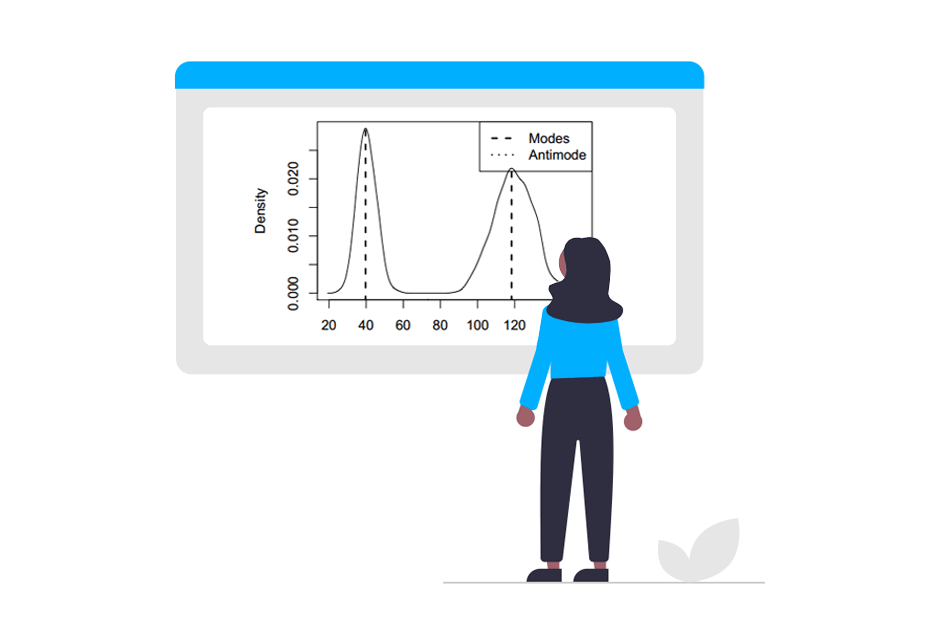
La librería también incorpora un método S3 para dibujar las estimaciones que devuelve la función locmodes, indicando la localización de las modas y de las antimodas, así como la ventana utilizada.

plot(modas)