Cuantiles en R

Considerando un valor \(p\), siendo \(0 < p < 1\), el cuantil de orden \(p\) es el valor que deja una proporción de los datos por debajo (\(p\)) y el resto \((1-p)\) por encima de ese valor. Observa que los cuantiles son la generalización de la mediana, que es el cuantil para \(p = 0.5\). En R, se puede hacer uso de la función quantile para calcular cualquier cuantil de cualquier vector numérico.

Sintaxis

La función quantile calcula los cuantiles muestrales de un vector numérico (x). Por defecto, esta función calcula los cuartiles especificados dentro de probs, pero también puedes introducir cualquier otra probabilidad para calcular cualquier percentil.

quantile(x,             # Vector numérico
         probs = seq(0, 1, 0.25), # Cuantiles (Por defecto los cuartiles: 0, 0.25, 0.5, 0.75, 1)
         na.rm = FALSE, # Si TRUE, elimina los datos faltantes
         names = TRUE,  # Si TRUE, el resultado tendrá nombres
         type = 7,      # Entero entre 1 y 9 para seleccionar un algoritmo para calcular los cuantiles
         digits = 7,    # Si names = TRUE, es el número de fígitos de los porcentages
         ...)           # Argumentos adicionales, de ser necesarios

Cuartiles

Los cuartiles son cuantiles de orden 0.25, 0.5 y 0.75 y dividen la muestra en cuatro partes con la misma frecuencia. Normalmente, los cuartiles se denotan por \(Q_1\), \(Q_2\) y \(Q_3\).

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular los cuartiles de x
quantile(x)

        0%        25%        50%        75%       100% 
-2.2146999 -0.4942425  0.1139092  0.6915454  2.4016178 

Recuerda que el cuartil 0.5 es igual a la mediana:

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular la mediana de x
median(x) # 0.1139092

Ten en cuenta que puedes eliminar los atributos de nombre de la salida pasando names = FALSE a la función.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular los cuartiles de x
quantile(x, names = FALSE)

-2.2146999 -0.4942425  0.1139092  0.6915454  2.4016178

Eliminar datos faltantes

Si tu vector numérico contiene datos faltantes no podrás calcular los cuantiles. Para solucionarlo necesitarás establecer na.rm = TRUE para eliminar los valores perdidos antes del cálculo.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Valor faltante
x[1] <- NA

# Calcular los cuartiles de x eliminando valores omitidos
quantile(x, na.rm = TRUE)

        0%        25%        50%        75%       100% 
-2.2146999 -0.4757753  0.1532533  0.6933514  2.4016178 

Algoritmos para estimar cuantiles

El cálculo de los cuantiles se basa en uno de los nueve algoritmos discutidos en Hyndman y Fan (1996). Por defecto, se utiliza el séptimo algoritmo, pero puedes seleccionar otro pasando un entero entre 1 y 9 a type. Lee la referencia anterior para más información sobre cada algoritmo.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular los cuartiles de x usando el algoritmo 8
quantile(x, type = 8)

        0%        25%        50%        75%       100% 
-2.2146999 -0.5156992  0.1139092  0.6939534  2.4016178 

Representación visual

Es importante tener en cuenta que se puedes utilizar un diagrama de caja y bigotes para visualizar los cuartiles, pero el método utilizado dentro de la función boxplot no es el mismo que el utilizado dentro de quartile, por lo que la salida puede variar ligeramente.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

quartile <- quantile(x)

# Box plot
boxplot(x, col = 4, horizontal = TRUE)
text(quartile[2], 1.25, expression(Q[1]))
text(quartile[3], 1.25, expression(Q[2]))
text(quartile[4], 1.25, expression(Q[3]))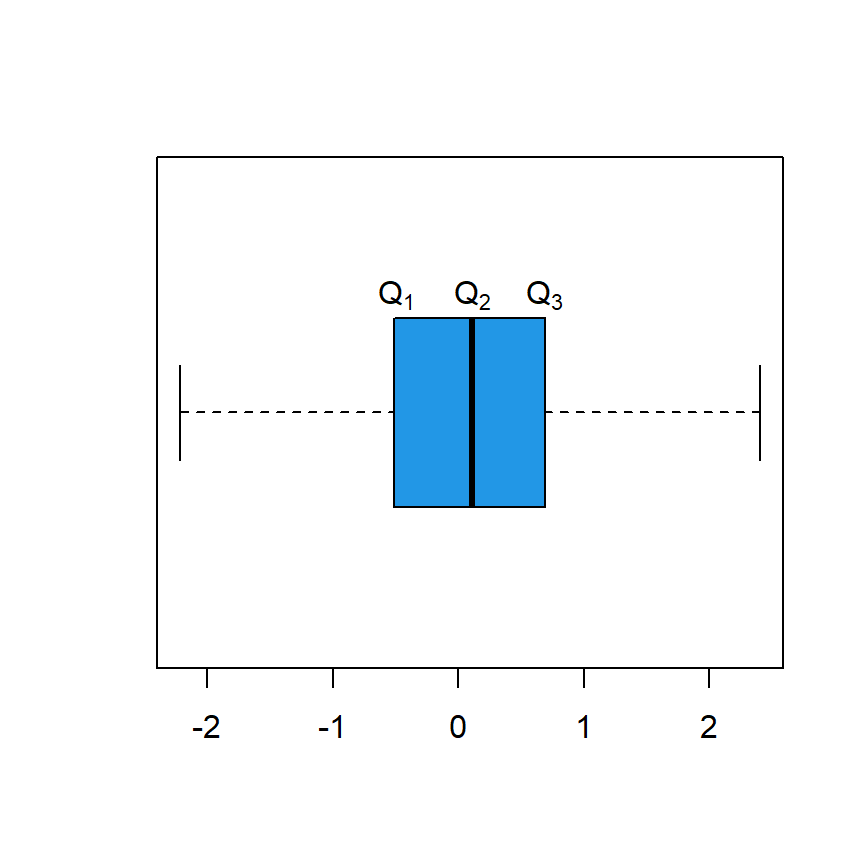

Deciles

Los deciles son cuantiles de orden 0.1, 0.2, …, 0.9 y dividen la muestra en 10 partes de igual frecuencia. Para calcularlos, puedes introducir una secuencia de 0 a 1 con paso 0.1 en probs, como se muestra en el siguiente ejemplo.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular los deciles de x
quantile(x, probs = seq(0, 1, by = 0.1))

         0%         10%         20%         30%         40%         50%         60%         70%         80%         90%        100% 
-2.21469989 -1.05265747 -0.61386923 -0.37534202 -0.07670313  0.11390916  0.37707993  0.58121734  0.77125360  1.18106508  2.40161776

Percentiles

Los percentiles son cuantiles del orden 0.01, 0.02, … , 0.99 y dividen la muestra en 100 partes de igual frecuencia. Si quieres calcular los percentiles de un vector numérico tendrás que especificar una secuencia de 0 a 1 con paso 0.01 dentro de probs.

# Datos de muestra
set.seed(1)
x <- rnorm(100)

# Calcular los percentiles de x
quantile(x, probs = seq(0, 1, by = 0.01))

          0%           1%           2%           3%           4%           5%           6%           7%           8% 
-2.214699887 -1.991605178 -1.808646490 -1.532008555 -1.472864961 -1.381744198 -1.282620249 -1.255240517 -1.226934278