Coeficiente de variación en R
El coeficiente de variación (CV) es una medida de dispersión utilizada para representar la variabilidad relativa de un conjunto de datos. Se calcula como la relación entre la desviación estándar y la media de un conjunto de datos, a menudo expresada en porcentaje.
Este coeficiente es una alternativa a la desviación típica, ya que permite comparar la variabilidad entre varios conjuntos de datos aunque tengan diferente escala o unidades de medida.
¿Cómo se calcula el coeficiente de variación?
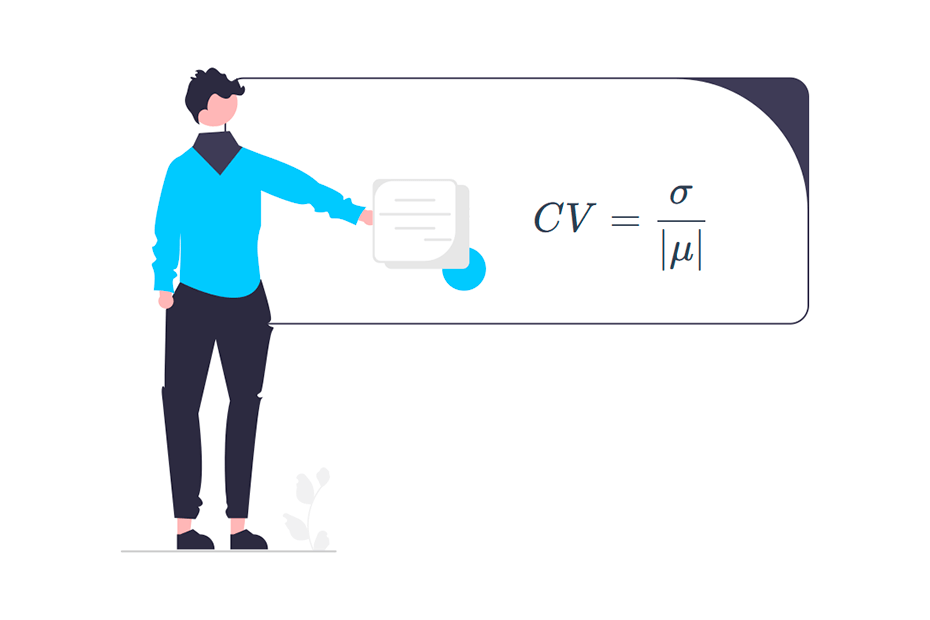
El coeficiente de variación poblacional (CV) es la relación entre la desviación típica y la media absoluta:
\[CV = \frac{\sigma}{|\mu|}\]
El coeficiente de variación se expresa a menudo en porcentaje, multiplicando el ratio por 100:
\[CV = \frac{\sigma}{|\mu|} \cdot 100\]
Para una muestra, se calcula como el cociente entre la desviación típica de la muestra (\(S\)) y la media de la muestra (\(\bar{X}\)):
\[CV = \frac{S}{|\bar{X}|}\]
Observa que la media debe ser diferente de 0.
En R, el coeficiente de variación de un conjunto de valores puede calcularse calculando el ratio entre la desviación típica (con la función sd) y la media (con la función mean).
# Datos de muestra
x <- c(10, 30, 3, 44, 12, 15)
# Desviación típica y media
sigma <- sd(x)
mu <- mean(x)
# Coeficiente de variación
cv <- sigma / abs(mu)
cv0.797503Si quieres calcular el coeficiente de variación en porcentaje sólo tienes que multiplicar el resultado anterior por 100:
# Datos de muestra
x <- c(10, 30, 3, 44, 12, 15)
# Desviación típica y media
sigma <- sd(x)
mu <- mean(x)
# Coeficiente de variación en porcentaje
cv <- sigma / abs(mu) * 100
cv79.7503Función para calcular el coeficiente de variación
Puedes crear tu propia función para calcular el coeficiente de variación de un conjunto de valores.
El siguiente bloque de código contiene una función llamada cv que toma un vector como entrada y proporciona dos argumentos adicionales: percentage para calcular el coeficiente como porcentaje cuando se establece en TRUE y na.rm para eliminar los valores faltantes si es necesario cuando se establece en TRUE.
# Función cv
cv <- function(x, percentage = TRUE, na.rm = FALSE) {
cv <- sd(x, na.rm = na.rm)/abs(mean(x, na.rm = na.rm)) * ifelse(percentage, 100, 1)
return(cv)
}Haciendo uso de la función anterior ahora puedes calcular el coeficiente de variación en una sola línea:
# Datos de muestra
x <- c(50, 48, 65, 13, 4, 19)
# Coeficiente de variación
cv(x, percentage = TRUE)73.54353Recuerde establecer percentage = FALSE si no quieres calcular el coeficiente como porcentaje:
# Datos de muestra
x <- c(50, 48, 65, 13, 4, 19)
# Coeficiente de variación
cv(x, percentage = FALSE)0.7354353Comparación del coeficiente de variación entre grupos
El principal caso de uso del coeficiente de variación es comparar la dispersión entre varios conjuntos de datos con diferentes escalas o unidades de medida. Considera los siguientes datos para dos grupos diferentes:
| grupo1 | grupo2 |
|---|---|
| 19 | 160 |
| 30 | 290 |
| 12 | 280 |
| 56 | 330 |
Como las escalas entre grupos son diferentes, si se calcula la desviación típica para cada grupo en el segundo grupo la desviación típica será mayor simplemente por su escala. Por tanto, no se podrá comparar la variabilidad entre grupos:
# Datos de muestra
df <- data.frame(grupo1 = c(19, 30, 12, 56),
grupo2 = c(160, 290, 280, 330))
# Desviación típica y media por grupo
s <- rbind(apply(df, 2, sd), apply(df, 2, mean))
rownames(s) <- c("sd", "mean")
s grupo1 grupo2
sd 19.31105 73.25754
mean 29.25000 265.00000Sin embargo, si se calcula el coeficiente de variación para cada grupo, la variabilidad puede compararse entre grupos, ya que este coeficiente es relativo.
# Datos de muestra
df <- data.frame(grupo1 = c(19, 30, 12, 56), grupo2 = c(160, 290, 280, 330))
# Coeficiente de variación para cada columna
# (utilizando la función 'cv' definida en la sección anterior)
apply(df, 2, cv) grupo1 grupo2
66.02069 27.64435Podemos concluir que el primer grupo tiene una variabilidad mayor (66.02%) que el segundo grupo (27.64%) a pesar de que la desviación típica del segundo grupo era mayor.