Tabla de contingencia en R

Estadística con R Asociación variables categóricas
Crea una tabla de contingencias en R con la función table y calcula las medidas de asociación

En varias situaciones resulta interesante estudiar dos o más variables al mismo tiempo. Al trabajar con variables categóricas, puedes resumir los datos en una tabla llamada tabla de contingencia. La relación entre las variables también se puede verificar con medidas de asociación. En este artículo aprenderás cómo crear una tabla de contingencia en R y cómo dibujar y verificar el grado de relación entre las variables con las medidas de asociación.

¿Cómo hacer una tabla de contingencia en R? La función table()

Las variables cualitativas, también conocidas como variables nominales, categóricas o de tipo factor, aparecen cuando se tienen variables no medibles (género, lugar de nacimiento, raza, …). Este tipo de variables se pueden representar con texto, donde cada nombre representa una única categoría, o con números, donde cada número representa una categoría única. Al trabajar con varias variables categóricas, puedes representar su distribución conjunta de frecuencias con una tabla de frecuencias o tabla de contingencia.

Considera el caso bidimensional con las variables nominales \(X\) e \(Y\) y denota \(x_i\), \(i = 1, \dots, k\) como los diferentes valores que pueden tomar la variable \(X\) e \(y_i\), \(i = 1, \dots, h\) como los valores que puede tomar la variable \(Y\). Con esto en mente podemos definir:

  1. Frecuencia absoluta conjunta de \((x_i, y_j)\). Es el número de individuos que representan al mismo tiempo los valores \(x_i \in X\) e \(y_j \in Y\) y se denota como \(n_{ij}\).
  2. Frecuencia relativa conjunta of \((x_i, y_j)\). Es la proporción de individuos que representan al mismo tiempo los valores \(x_i \in X\) e \(y_j \in Y\) del número total de individuos y se define como \(f_{ij}=n_{ij}/n\), donde \(n\) es el tamaño muestral.

Ten en cuenta que la distribución bidimensional es el conjunto de valores que la variable bidimensional $ (X, Y)$ puede tomar además de las frecuencias conjuntas de esos valores. Para representar una distribución bidimensional, puedes usar una tabla de contingencia bidimensional, conocida como tabla de dos vías o de dos entradas, que toma la forma:

\(X\) \ \(Y\) \(y_1\) \(y_2\) \(\dots\) \(y_j\) \(\dots\) \(h_h\) \(n_{j \bullet}\)
\(x_1\) \(n_{11}\) \(n_{12}\) \(\dots\) \(n_{1j}\) \(\dots\) \(n_{1h}\) \(n_{1 \bullet}\)
\(x_2\) \(n_{21}\) \(n_{22}\) \(\dots\) \(n_{2j}\) \(\dots\) \(n_{2h}\) \(n_{2 \bullet}\)
\(\vdots\) \(\vdots\) \(\vdots\) \(\ddots\) \(\dots\) \(\ddots\) \(\vdots\) \(\vdots\)
\(x_i\) \(n_{i1}\) \(n_{i2}\) \(\dots\) \(n_{ij}\) \(\dots\) \(n_{ih}\) \(n_{i \bullet}\)
\(\vdots\) \(\vdots\) \(\vdots\) \(\ddots\) \(\dots\) \(\ddots\) \(\vdots\) \(\vdots\)
\(x_k\) \(n_{k1}\) \(n_{k2}\) \(\dots\) \(n_{kj}\) \(\dots\) \(n_{kh}\) \(n_{k \bullet}\)
\(n_{\bullet j}\) \(n_{\bullet 1}\) \(n_{\bullet 2}\) \(\dots\) \(n_{\bullet j}\) \(\dots\) \(n_{\bullet h}\) \(n\)

Tabla de frecuencias absolutas en R

Puedes hacer uso de la función table para crear una tabla de contingencia en R. Considera, como ejemplo, el siguiente conjunto de datos aleatorios, donde la variable \(X\) representa los votos a favor (Si) y en contra (No) de una ley en un comité internacional compuesto por miembros de tres continentes (variable \(Y\)):

# Fijamos semilla
set.seed(20)

# Generamos datos aleatorios para la variable X
X <- sample(c("Si", "No"), 10, replace = TRUE)
# "No" "Si" "Si" "No"  "No" "Si" "No" "Si" "No" "No"

# Generamos datos aleatorios para la variable Y
Y <- sample(c("Europa", "America", "Africa"), 10, replace = TRUE)
# "Europa" "Africa"  "Africa"  "Europa"  "Africa" 
# "Europa" "Europa"  "Europa"  "America" "America"

tabla <- table(X, Y)
tabla

Con la función table puedes crear una tabla de frecuencias (la distribución marginal) para cada variable:

table(X)
# X
#  No  Si 
#   6   4 
table(Y)
# Y
#  Africa America  Europa 
#       3       2       5

Sin embargo, si pasas dos variables a la función, puedes crear una tabla de contingencia de dos entradas. Cabe mencionar que podrías agregar más variables a la función, dando como resultado un array multidimensional.

     Y
X      Africa  America  Europa
  No       1       2      3
  Yes      2       0      2

Además, puedes modificar los nombres de las columnas y de las filas con las funciones colnames y rownames, respectivamente.

rownames(tabla) <- c("0", "1")
colnames(tabla) <- c("Af", "Am", "Eu")
tabla
   Y
X   Af Am Eu
  0  1  2  3
  1  2  0  2

También puedes convertir un data frame o una matriz en una tabla. Para ello, puedes utilizar la función as.table.

Tabla de frecuencias relativas en R

La tabla creada con la función table muestra la frecuencia absoluta conjunta de las variables. No obstante, puedes obtener la frecuencia relativa conjunta en R (como fracción de una tabla marginal) con la función prop.table. Por defecto, la función calcula la proporción de cada celda con respecto al total de observaciones, por lo que la suma de las celdas es igual a 1.

tabla_prop <- prop.table(tabla)
tabla_prop
     Y
X     Africa  America  Europa
  No     0.1     0.2    0.3
  Yes    0.2     0.0    0.2

Sin embargo, el argumento margin permite seleccionar el índice (1: filas, 2: columnas) según el cual se van a calcular las proporciones.

Por una parte, si estableces margin = 1, la suma de cada fila será igual a 1.

prop.table(tabla, margin = 1)
     Y
X        Africa   America    Europa
  No  0.1666667 0.3333333 0.5000000
  Yes 0.5000000 0.0000000 0.5000000

Por otra parte, si estableces margin = 2, la frecuencia relativa se calculará por columnas, por lo que cada columna sumará 1.

tabla_2 <- prop.table(tabla, margin = 2)
tabla_2 
     Y
X        Africa   America    Europa
  No  0.3333333 1.0000000 0.6000000
  Yes 0.6666667 0.0000000 0.4000000

Ten en cuenta que también puedes agregar los márgenes a una tabla de contingencia en R con la función addmargins, para mostrar la frecuencia relativa acumulada (o la frecuencia absoluta acumulada, si se aplica a una tabla de frecuencias absoluta). En el siguiente ejemplo calculamos los márgenes de tabla_prop, expresando los datos como porcentaje.

tabla_3 <- addmargins(tabla_prop * 100)
tabla_3
     Y
X      Africa  America  Europa Sum
  0       10      20      30    60
  1       20       0      20    40
  Sum     30      20      50   100

Gráficos de tablas de contingencia de dos entradas

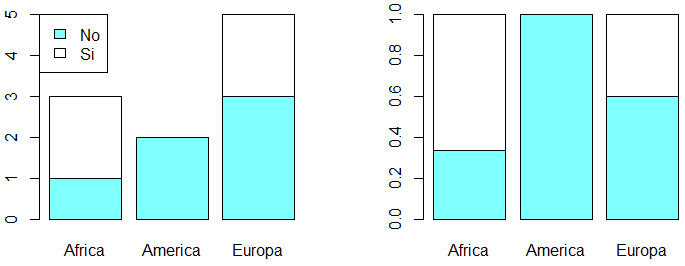
Para dibujar una tabla en R, puedes utilizar los gráficos de barras, que se pueden crear con la función barplot. Hay dos tipos principales: agrupados y apilados. Por defecto, la función creará un diagrama de barras apiladas:

# Dividimos la ventana gráfica en dos columnas
par(mfrow = c(1, 2))

colores <- c("#80FFFF", "#FFFFFF")

barplot(tabla, col = colores)

# Añadimos una leyenda
legend("topleft", legend = c("No", "Si"), fill = colores)

barplot(tabla_2, col = colores)

# Volvemos a la ventana gráfica original
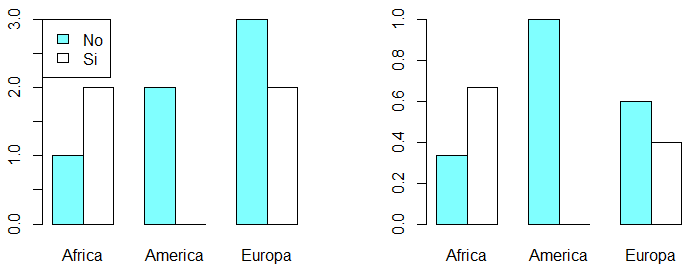
par(mfrow = c(1, 1))

Gráfico tabla de contingencia de dos entradas o dos vías

Si prefieres un gráfico de barras agrupadas, deberás establecer el argumento beside como TRUE:

par(mfrow = c(1, 2))

barplot(tabla, col = colores, beside = TRUE)
legend("topleft", legend = c("No", "Si"), fill = colores)
barplot(tabla_2, col = colores, beside = TRUE)

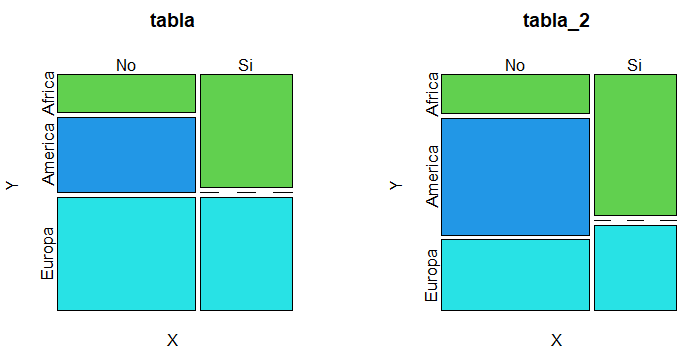
par(mfrow = c(1, 1))

Gráfico tabla en R

Una alternativa a los diagramas de barras son los gráficos de mosaico, que permiten mostrar dos o más variables categóricas. Este tipo de diagrama se puede crear en base R con la función mosaicplot de la siguiente manera:

par(mfrow = c(1, 2))

mosaicplot(tabla, cex = 1.1, col = 3:5)
mosaicplot(tabla_2, col = 3:5)

par(mfrow = c(1, 1))

Gráfico de mosaico de una tabla con la función mosaicplot de R

Si todos los cuadros en todas las categorías tienen la misma área estamos ante una señal de independencia.

Medidas de asociación en R

Se puede comprobar que las variables son dependientes, si existe alguna relación entre ellas, o independientes en caso contrario. Para definir la condición de independencia, si $ X$ es independiente de $ Y$ podemos verificar que para todo $ i$:

\(\frac{n_{i1}}{n_{\bullet 1}} = \frac{n_{i2}}{n_{\bullet 2}} = \dots = \frac{n_{ij}}{n_{\bullet j}} = \dots = \frac{n_{ih}}{n_{\bullet h}} = \frac{n_{i \bullet}}{n}.\)

Lo anterior es equivalente a:

\(\frac{n_{i j}}{n} = \frac{n_{i \bullet}}{n} \frac{n_{\bullet j}}{n} \quad \forall i, j.\)

Coeficiente Chi-cuadrado en R

Puedes verificar la independencia con la prueba de chi-cuadrado, comparando las frecuencias esperadas \(e_{ij}\) con \(n_{ij}\). La medida Chi-cuadrado es:

\(\chi^2 = \sum_{i, j} \frac{(n_{ij} - e{ij})^2}{e_{ij}}.\)

Ten en cuenta que esta variable proporciona, en términos relativos, la distancia entre la distribución conjunta de las variables del caso de independencia. Por lo tanto, cuanto mayor sea el valor de $ ^ 2$, mayor será la asociación entre las variables. Esta medida va de 0 (independencia) a $ n (q-1)$, siendo $ q$ el mínimo entre el número de filas y columnas.

Sin embargo, como esta métrica no está acotada entre 0 y 1, existen otras medidas de asociación, que se describen en las subsecciones siguientes.

Puedes obtener el coeficiente Chi-cuadrado en R con la función chisq.test como sigue:

chi <- chisq.test(tabla)
chi$statistic
X-squared 
 2.222222

Por tanto, en este caso, el valor del coeficiente Chi-cuadrado es 2.2222.

Coeficiente de contingencia

El coeficiente de contingencia C está limitado entre 0 (caso de independencia) y 1. Se define como:

\(C = \sqrt{\frac{\chi^2}{\chi^2 + n}}.\)

Para calcular el coeficiente de contingencia en R, puedes utilizar la siguiente función:

Contingency <- function(x) {
    chi <- chisq.test(x)
    unname(sqrt(chi$statistic / (chi$statistic + sum(x))))
}
Contingency(tabla) # 0.4264014

Una alternativa es usar la función ContCoef del paquete DescTools:

# install.packages("DescTools")
library(DescTools)

ContCoef(tabla) # 0.4264014

El valor máximo que puede tomar el coeficiente de contingencia es \(\sqrt{(k-1) / k}\), por lo que el valor 1 nunca se alcanza para tablas cuadradas. Sea \(k\) el número de filas y $ h$ el número de columnas, algunos valores que puede tomar el coeficiente son:

k = h 2 3 4 5 6
max C 0.71 0.82 0.87 0.89 0.91

Coeficientes Phi y V de Cramer

El coeficiente Phi se define como:

\(\phi = \sqrt{\frac{\chi^2}{n}}.\)

Ten en cuenta que toma valores entre 0 y 1 en las tablas 2×2. Sin embargo, puede tomar valores mayores que 1 en otros casos. Para evitar este problema, el coeficiente V de Cramer modifica el coeficiente Phi, tomando la forma:

\(V = \sqrt{\frac{\chi^2}{[n(q - 1)]}}.\)

Recuerda que \(q\) es el mínimo entre el número de filas y de columnas.

En R puedes utilizar las siguientes funciones para calcular estos coeficientes:

# Coeficiente Phi
PhiCoef <- function(x){
    unname(sqrt(chisq.test(x)$statistic / sum(x)))
}

# Coeficiente V de Cramer
V <- function(x) {
    unname(sqrt(chisq.test(x)$statistic / (sum(x) * (min(dim(x)) - 1))))
}
PhiCoef(tabla) # 0.4714045
V(tabla)   # 0.4714045

Una alternativa es usar las funciones Phi y CramerV del paquete DescTools.

# install.packages("DescTools")
library(DescTools)

Phi(tabla) # 0.4714045
CramerV(tabla) # 0.4714045

Como comentario final, cabe mencionar que puedes calcular varias medidas de asociación en R al mismo tiempo con la función assocstats de la biblioteca vcd.

# install.packages("vcd")
library(vcd)

assocstats(tabla)
                    X^2 df P(> X^2)
Likelihood Ratio 2.9110  2  0.23328
Pearson          2.2222  2  0.32919

Phi-Coefficient   : NA 
Contingency Coeff.: 0.426 
Cramer's V        : 0.471