Covarianza y correlación en R
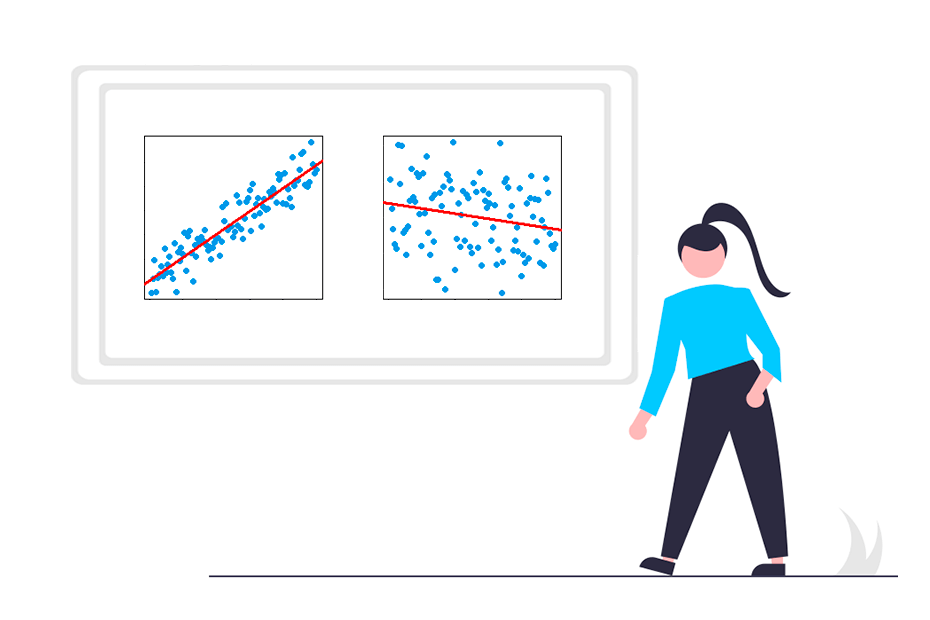
Las funciones cor y cov son útiles para analizar relaciones entre variables, pero mientras la primera calcula el coeficiente de correlación, la segunda calcula la covarianza.
Consulta el tutorial sobre gráficos de correlación para aprender a visualizar este tipo de datos.
Sintaxis
La sintaxis de ambas funciones es la misma:
# Covarianza
cov(x, y = NULL, use = "everything",
method = c("pearson", "kendall", "spearman"))
# Correlación
cor(x, y = NULL, use = "everything",
method = c("pearson", "kendall", "spearman"))Siendo:
x,y: vectores, data frames o matrices que contienen datos numéricos.use: determina cómo manejar los valores faltantes. Por defecto es"everything", pero también se puede establecer como"complete.obs","pairwise.complete.obs", o"na.or.complete".method: especifica el método para calcular el coeficiente de correlación. Las posibles opciones son"pearson"(por defecto),"kendall", o"spearman".
Covarianza
La covarianza es una métrica de variación conjunta que indica si existe relación lineal entre las variables. Este coeficiente se suele denotar como \(S\) y su interpretación es la siguiente:
- Si \(S > 0\), existe una relación positiva.
- Si \(S \approx 0\), no existe relación.
- Si \(S < 0\), existe una relación negativa.
Además, cuanto mayor sea el coeficiente de covarianza, mayor será la relación.
La magnitud de la covarianza no es fácilmente interpretable porque no está acotada y está influida por las escalas de las variables.
En R, la función cov puede utilizarse para calcular el coeficiente de covarianza entre dos vectores numéricos:
# Datos de muestra
set.seed(15)
x <- rnorm(100)
y <- x + rnorm(100)
# Covarianza entre x e y
cov(x, y)1.028619La función devuelve un valor de 1.028619, lo que indica una relación lineal positiva entre \(x\) e \(y\).
Matriz de covarianzas
Si la entrada de la función es una matriz numérica o data frame en lugar de dos vectores numéricos, la función calculará las covarianzas entre las columnas del conjunto de datos.
# Datos de muestra
set.seed(15)
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100), Var3 = rexp(100))
# Matriz de covarianzas de 'df'
cov(df) Var1 Var2 Var3
Var1 0.98795201 -0.024517909 -0.079986687
Var2 -0.02451791 0.084020062 -0.009591341
Var3 -0.07998669 -0.009591341 2.118357213También puedes introducir dos data frames o matrices para calcular la correlación entre las columnas de los conjuntos de datos.
# Datos de muestra
set.seed(15)
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100), Var3 = rexp(100))
df2 <- data.frame(Var4 = rnorm(100), Var5 = runif(100), Var6 = rexp(100))
# Matriz de covarianzas entre 'df' y 'df2'
cov(df, df2) Var4 Var5 Var6
Var1 -0.001427763 0.014351821 -0.05569541
Var2 0.041006100 0.005160602 -0.06376888
Var3 0.064429874 -0.053229349 0.03178257Correlación
El principal problema de la covarianza es que no está acotada y depende de las unidades de medida. Para resolver estos problemas, existe el coeficiente de correlación, normalmente denotado como \(r\), que es una métrica adimensional que varía entre -1 y 1.
- Si \(r = 1\), implica que existe una relación positiva perfecta.
- Si \(r > 0\), implica una relación positiva.
- Si \(r \approx 0\), no hay correlación entre las variables.
- Si \(r < 0\), implica una relación negativa.
- Si \(r = - 1\), existe una relación positiva perfecta.
El coeficiente de correlación puede calcularse con la función cor.
Coeficiente de correlación de Pearson
El coeficiente de correlación por defecto calculado por cor se llama coeficiente de correlación de Pearson. En el siguiente ejemplo estamos calculando el coeficiente de correlación para \(x\) e \(y\):
# Datos de muestra
set.seed(15)
x <- rnorm(100)
y <- x + rnorm(100)
# Coeficiente de correlación entre x e y
cor(x, y)0.6856568La función devuelve un coeficiente de 0.6856568, lo que indica una fuerte relación positiva entre las dos variables.
Coeficiente tau de Kendall
El coeficiente de correlación de Kendall, también conocido como \(\tau\) de Kendall, es adecuado para datos ordinales o distribuidos de forma no normal, ya que se basa en el rango u orden de los valores en lugar de en los valores reales. Establece method = "kendall" para calcularlo.
# Datos de muestra
set.seed(15)
x <- rnorm(100)
y <- x + rnorm(100)
# Coeficiente de correlación de Kendall entre x e y
cor(x, y, method = "kendall")0.4840404La función devuelve un coeficiente de 0.4840404, lo que implica una relación positiva entre \(x\) e \(y\).
Coeficiente rho de Spearman
El coeficiente de correlación de Spearman (\(\rho\) de Spearman) es una alternativa robusta y no paramétrica del coeficiente de Pearson, también basado en el rango de valores como la \(\tau\) de Kendall. Se suele utilizar cuando los datos no son normales o tienen valores atípicos, ya que capta mejor las posibles relaciones no lineales entre variables. Establece method = "spearman" para calcularlo.
# Datos de muestra
set.seed(15)
x <- rnorm(100)
y <- x + rnorm(100)
# Coeficiente de correlación de Spearman entre X e Y
cor(x, y, method = "spearman")0.6706871La función devuelve un coeficiente de 0.6706871, muy similar al coeficiente de Pearson, lo que también indica una fuerte relación positiva entre las dos variables.
El coeficiente de Spearman es la mejor opción cuando los datos no son normales o presentan valores atípicos.
Matriz de correlación
Si introduces un data frame o matriz con varias columnas a cor, dicha función calculará la matriz de correlaciones para las variables, como se ilustra en el siguiente ejemplo.
# Datos de muestra
set.seed(15)
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100), Var3 = rexp(100))
# Matriz de correlación de 'df'
cor(df) Var1 Var2 Var3
Var1 1.00000000 -0.08509891 -0.05529046
Var2 -0.08509891 1.00000000 -0.02273465
Var3 -0.05529046 -0.02273465 1.00000000También puedes pasar dos data frames o matrices para calcular la correlación entre las columnas del primer conjunto de datos con las columnas del segundo.
# Datos de muestra
set.seed(15)
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100), Var3 = rexp(100))
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100))
# Matriz de correlación entre 'df' y 'df2'
cor(df, df2) Var4 Var5 Var6
Var1 1.00000000 -0.03199334 -0.11915007
Var2 -0.03199334 1.00000000 0.04328424
De matriz de covarianzas a matriz de correlación con cov2cor
R también proporciona una función útil llamada cov2cor que permite transformar una matriz de covarianzas en una matriz de correlación de manera eficiente. La función toma una matriz de covarianzas como entrada, como se muestra a continuación.
# Datos de muestra
set.seed(15)
df <- data.frame(Var1 = rnorm(100), Var2 = runif(100), Var3 = rexp(100))
# Matriz de covarianzas de 'df'
S <- cov(df)
# Transformar la matriz de covarianzas a matriz de correlación
cov2cor(S) Var1 Var2 Var3
Var1 1.00000000 -0.08509891 -0.05529046
Var2 -0.08509891 1.00000000 -0.02273465
Var3 -0.05529046 -0.02273465 1.00000000